الكرة الأرضية

English المواضيع
positional

الكرة الأرضية

​

سنبدأ بتعريف كرة مألوفة: الأرض (سنفترض مبدئياً أنها كروية), تدور حول محور .

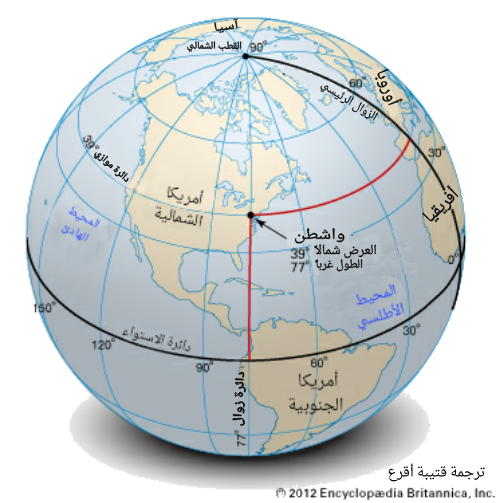(الشكل-1) الإحداثيات الجغرافية الأرضية

القطبين الشمالي & الجنوبي هي النقاط التي تلتقي فيها هذه الأقطاب مع سطح الأرض. يقع خط الاستواء في منتصف المسافة بينهما.

خط الاستواء ما هو إلا مثال للدائرة الكبرى: و التي يمر مستويها بمركز الكرة. لكل دائرة كبرى قطبين. و يمكن تعريفها بهذين التعريفين: (a) هي النقاط على الكرة و التي تبعد عن دائرة بمقدار 90°. (b) هي النقاط التي يحددها الخط المعامد لمستوي الدائرة الكبرى و الذي يخترق سطح الكرة لتلك الدائرة. إن هذين التعريفين متكافئين.

(الشكل-2) الدوائر الصغرى و الكبرى

يعرف طول القوس للدائرة الكبرى على سطح الكرة بأنه الزاوية بين نقطتي نهايتيه، و ذلك كما يبدو من مركز الكرة، و يقدر بالدرجات ( لا يقاس بالأميال و لا بالكيلومتر ... إلخ).

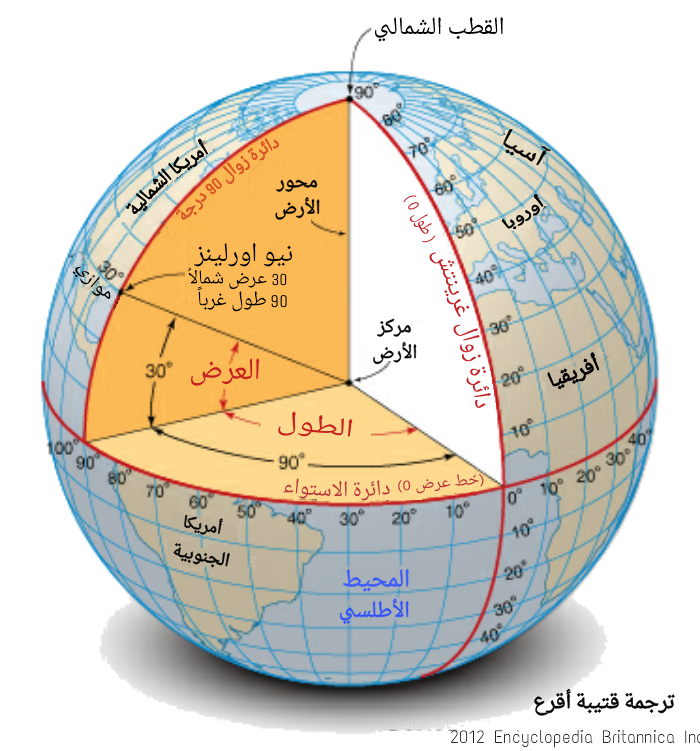(الشكل-3) الإحداثيات الجغرافية

الدائرة الكبرى هي خط جيوديزي (و هو الخط الأقصر الواصل بين نقطتين) على سطح كرة و هو يماثل الخط المستقيم على سطح مستوي.

لوصف موضع نقطة X على سطح كرة الأرض، نستخدم العرض و الطول ( و هما إحداثيين اثنين، و يعود ذلك لكون سطح الكرة ثنائي البعد).

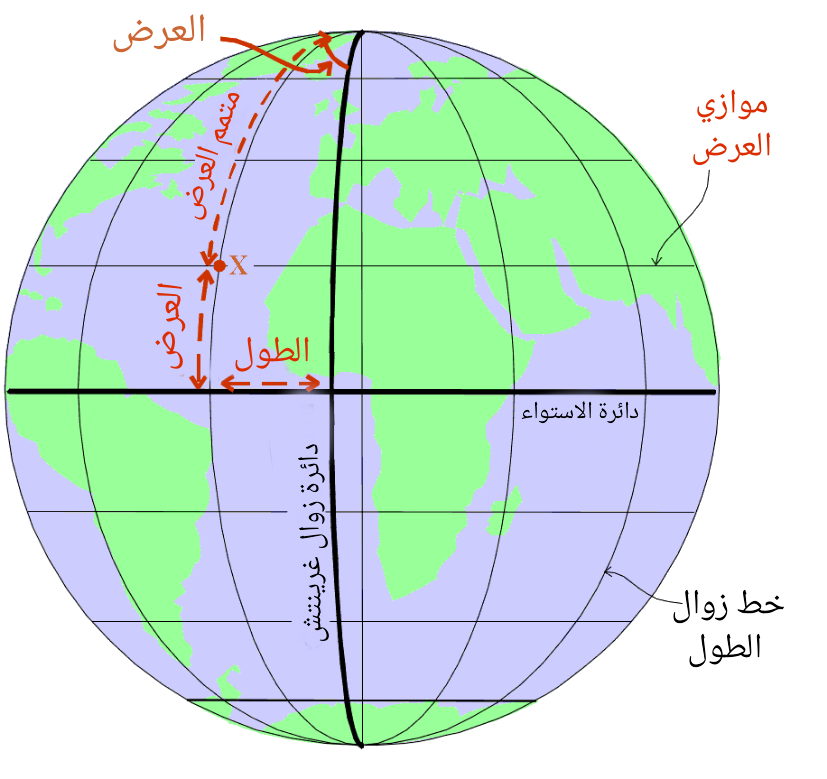(الشكل-4) خط الزوال و خط الموازي

قم برسم دائرة كبرى من القطب إلى القطب بحيث تمر من الموضع X:و تدعى دائرة زوال الطول.

يعرف العرض Φللموضع X بأنه البعد الزاوي عبر خط الزوال هذا بدءا من دائرة الاستواء و حتى الموضع X, و يقاس من -90° للقطب الجنوبي و إلى +90° للقطب الشمالي.

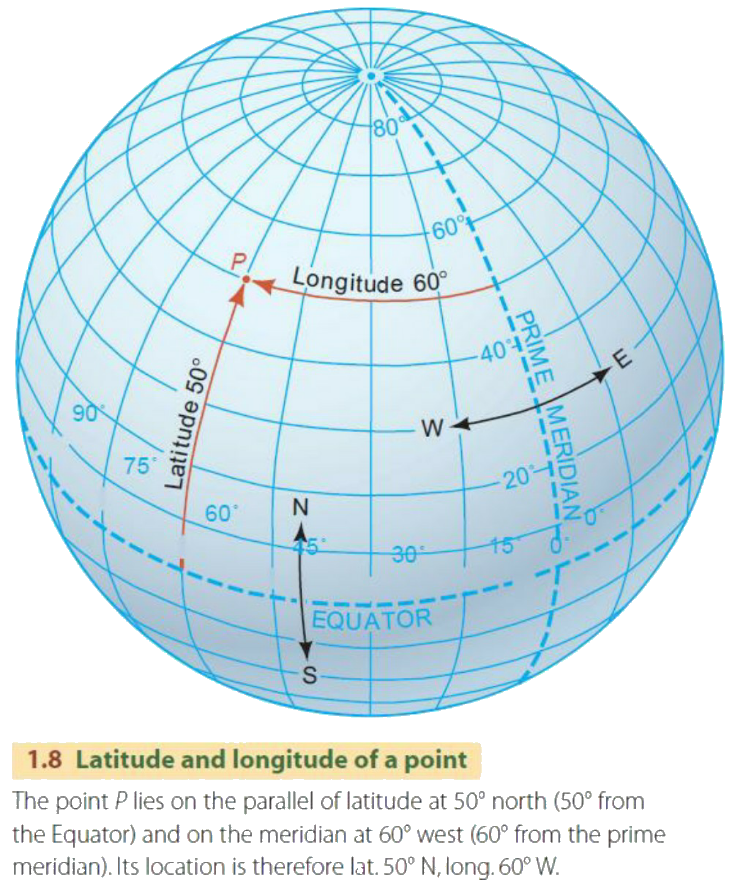
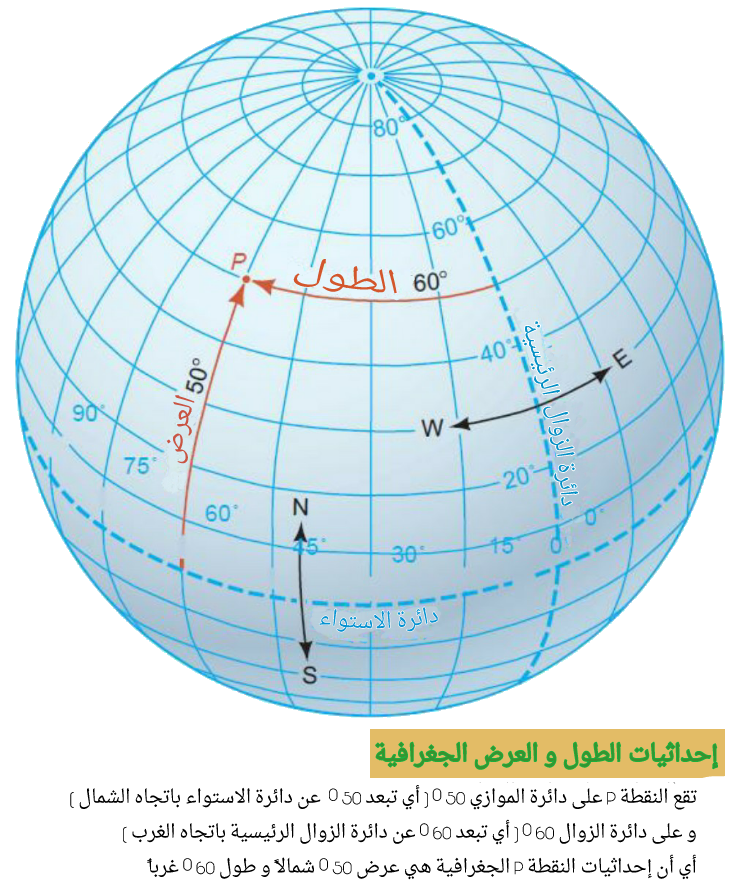(الشكل-5) توضيح معنى إحداثيات نقطة

يعرف متمم العرض للموضع X بأنه البعد الزاوي للنقطة X عن القطب الشمالي و تساوي

متمم العرض = 90° - العرض.

لا يوجد نقطة مميزة تعد مرجعاً قياسياً للطول ; و لاسباب تاريخية تم اختيار خط زوال يمر بمدينة غرينتش و هو خط الصفر المبدأ لخطوط الطول (و يدعى أيضاً خط الزوال الرئيسي).

(الشكل-6) دوائر الطول و العرض على سطح الأرض

الطول λ للموضع X هو البعد الزاوي عبر دائرة الاستواء بدءاً من دائرة الزوال الرئيسية وصولاً إلى دائرة الزوال المارة بالموضع X. و تقاس شرقاً أو غرباً من قيمة 0° و حتى القيمة 360°, أو في كلا الاتجاهين من 0° و حتى 180°.

تدعى الدوائر الصغيرة الموازية لخط الاستواء موازيات العرض .

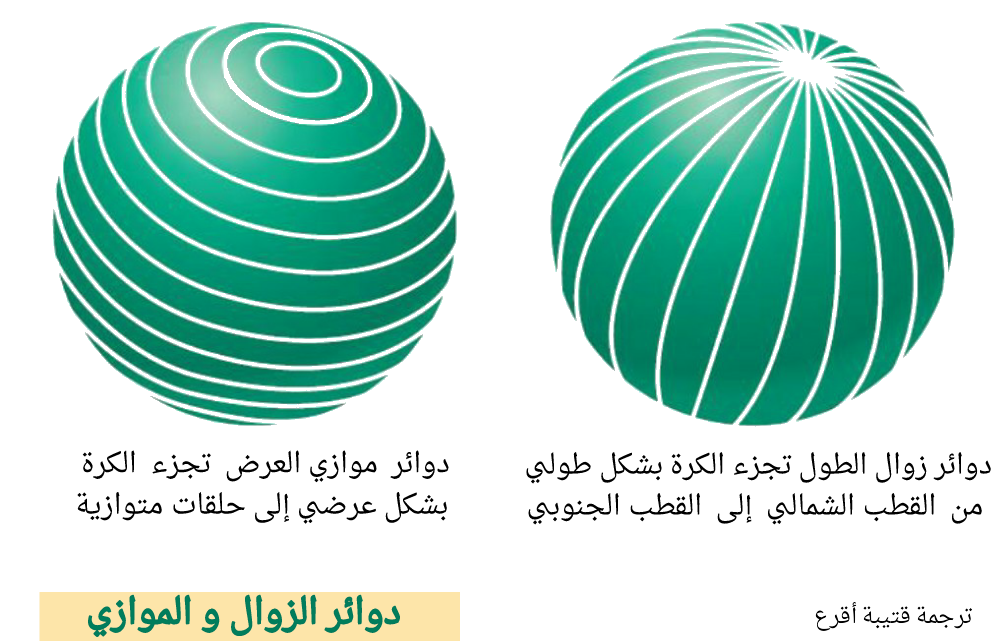(الشكل-7) دوائر الزوال و الموازي


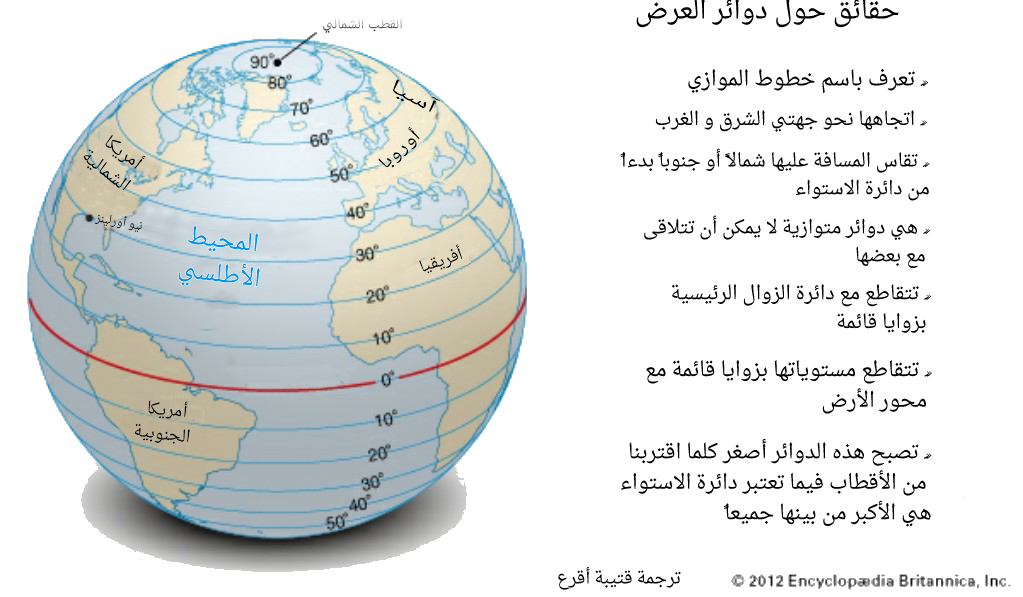(الشكل-8) بعض الحقائق حول دوائر العرض

إن محيط أي دائرة خط عرض يساوي:

= 360 ✗ cos( مقدراً بالدرجات ( العرض.

يحسب طول القوس للدائرة الصغرى بين زوالين طوليين

= (الفرق في الطول) ✗ cos(العرض)

المسافة على الدائرة الكبرى هو دائماً أقل من هذا كما سنرى في القسم التالي.

تذكر بأن الموضع على سطح الأرض ثابت بالعودة الى استخدام دائرة رئيسية واحدة (دائرة الاستواء) و عليه تتوضع نقطة ثابتة واحدة (و هي نقطة تقاطعه مع زوال خط غرينتش).

flash animation

الملاحة السماوية تستخدم في الإبحار( و كذلك في الملاحة الجوية) حيث تستخدم الهندسة الكروية, و تكون النتائج بقيم زاوية ( درجات). و يجب القيام بتحويل هذه القيم إلى قيم خطية للاستخدام العملي. و يعرف الميل البحري بأنه يساوي دقيقة-قوسية واحدة على طول الدائرة الكبرى على الأرض. و هذا يعطي زيادة 15% عن القيمة العادية "القانونية" للميل (6080 قدم بدلاً من 5280 قدم).

تمرين:

Alderney, هي مدينة في جزر الشانيل تقع على

خط طول 2°W و خط عرض 50°N.

Winnipeg, مدينة كندية, تقع على

خط طول 97°W و خط عرض 50°N

كم تبلغ المسافة بينهما مقدرة بالميل البحري, على امتداد خط العرض الموازي؟

الحل

تعرف المسافة على امتداد العرض الموازي :



و لكننا نعرف أن

1° = 60 ميلاً بحرياً.

لذلك المسافة تكون


61.06 ✘ 60 =3663 ميل بحري.

ملاحظة: الاحداثيات الأرضية هي أكثر تعقيداً في الواقع من هذه التعاريف, و ذلك يعود لكون الأرض ليست كروية تماماً. و يمكنك الرجوع لهذه الروابط من أجل المزيد حول Ordnance Survey's:

Terrestrial Sphere

Arabic Index
positional

The Terrestrial Sphere

Start with a familiar sphere: the Earth (assume for the moment that it is spherical), spinning around an axis.

(Figure-1) Geographical coordinates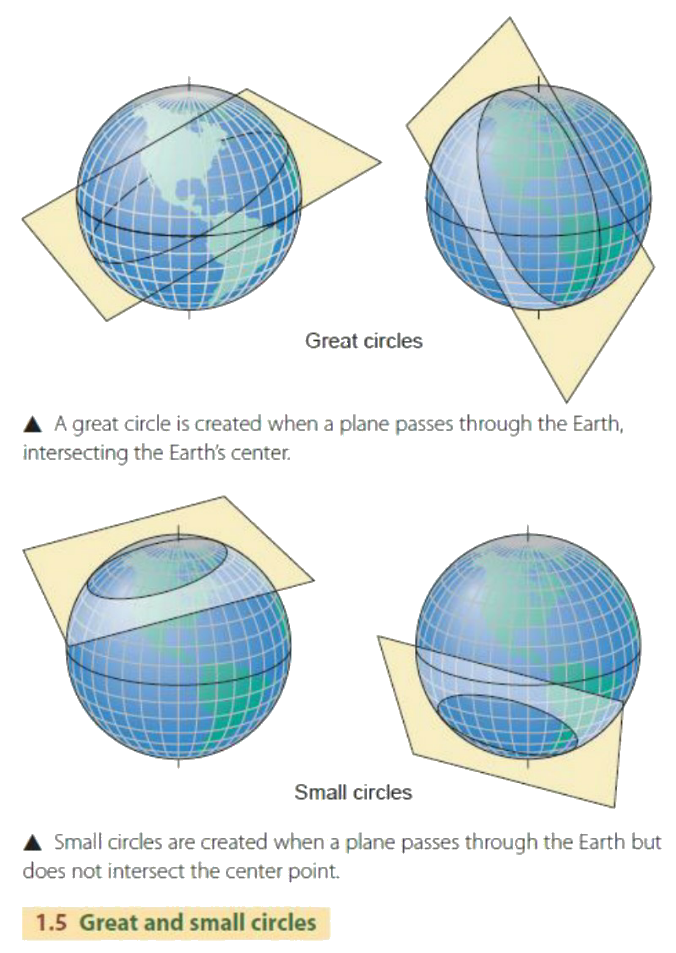

The North & South Poles are where this axis meets the Earth's surface. The equator lies midway between them.

The equator is an example of a great circle: one whose plane passes through the centre of the sphere. Every great circle has two poles. We can define these: (a) as the points which are 90° away from the circle, on the surface of the sphere. (b) as the points where the perpendicular to the plane of the great circle cuts the surface of the sphere. These two definitions are equivalent.

(Figure-2) Great and Small Circles

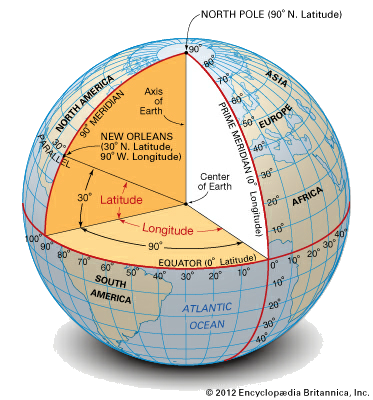The length of a great-circle arc on the surface of a sphere is the angle between its end-points, as seen at the centre of the sphere, and is expressed in degrees (not miles, kilometres etc.).

(Figure-3) Geographical Coordinates

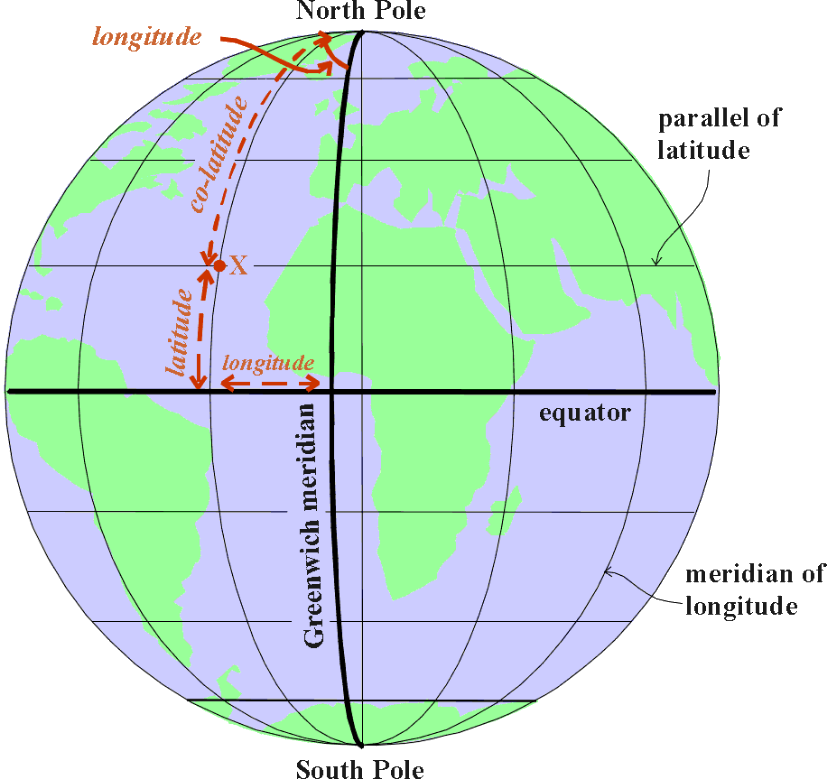A great circle is a geodesic (the shortest distance between two points) on the surface of a sphere, analogous to a straight line on a plane surface.

To describe a location X on the surface of the Earth, we use latitude and longitude (two coordinates, because the surface is two-dimensional).

(Figure-4) Meridian and the parallel of Latitude

Draw a great circle from pole to pole, passing through location X: this is a meridian of longitude.

The latitude of X is the angular distance along this meridian from the equator to X, measured from -90° at the South Pole to +90° at the North Pole.

(Figure-5) Coordinates of Point on the earth surface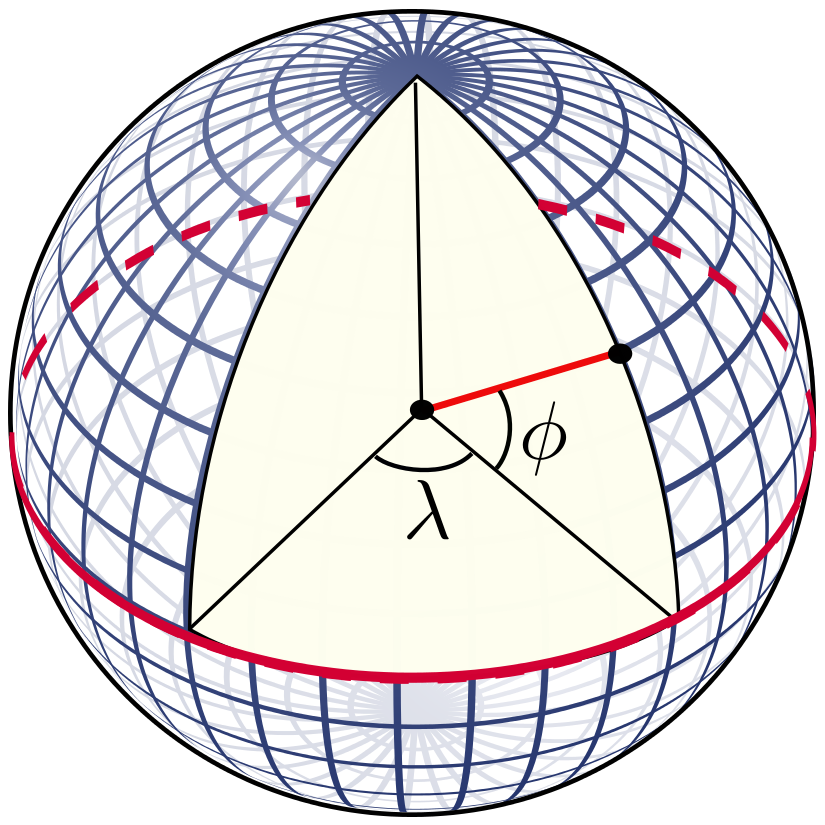

The co-latitude of X is the angular distance from the North Pole to X

co-latitude= 90° - latitude.

There is no obvious point of origin for measuring longitude; for historical reasons, the zero-point is the meridian which passes through Greenwich (also called the Prime Meridian).

(Figure-6) Longitude & Latitude Circles

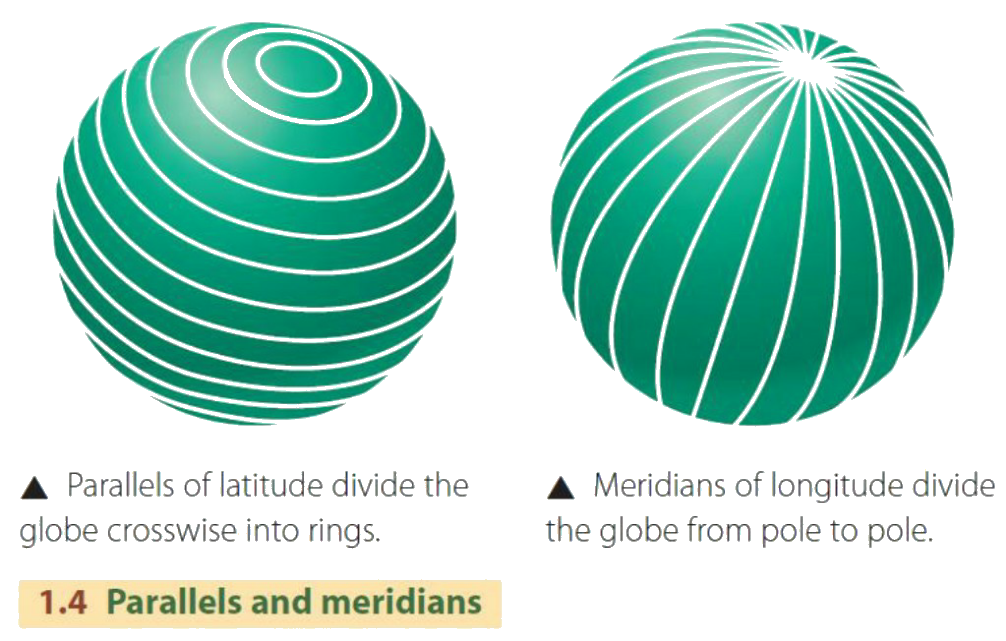The longitude of X is the angular distance along the equator from the Prime Meridian to the meridian through X. It may be measured east or west 0° to 360°, or both ways 0° to 180°.

Small circles parallel to equator are parallels of latitude. The circumference of a small circle at any given latitude is:

(Figure-7) Meridian & Parallel Circles


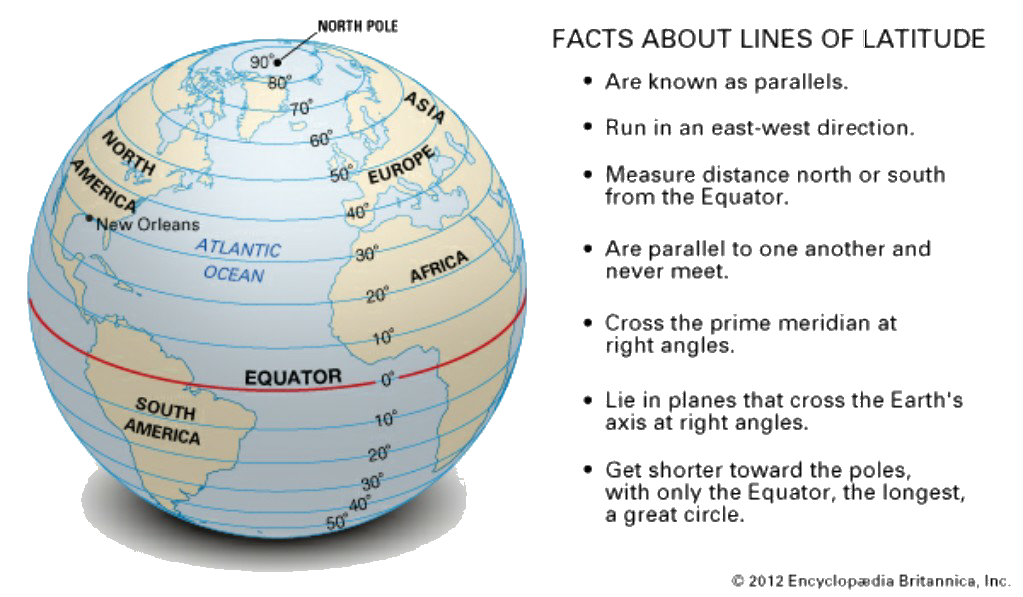(Figure-8) facts about Latitude Lines

circumference=360✗cos(latitude) degrees.

The length of arc of a small circle between two meridians of longitude is

(difference in longitude) ✗ cos(latitude)

.

The great-circle distance is always less than this, as we shall see in the next section.

Note that a position on the surface of the Earth is fixed using one fundamental circle (the equator) and one fixed point on it (the intersection with Greenwich Meridian).

flash animation

Celestial navigation used at sea (and in the air) involves spherical trigonometry, so the results are in angular measure (degrees). These must be converted to linear measure for practical use. We define the nautical mile as 1 arc-minute along a great circle on Earth's surface. This comes out about 15% greater than the normal "statute" mile (6080 feet instead of 5280 feet).

Exercise:

Alderney, in the Channel Islands, has

longitude 2°W, latitude 50°N.

Winnipeg, in Canada, has

longitude 97°W, latitude 50°N.

How far apart are they, in nautical miles, along a parallel of latitude?

Answer

Distance along a parallel of latitude is

=(difference in longitude) ✗ cos(latitude)

= (97° - 2°)✗cos(50°) = 61.06°

But 1° = 60 nautical miles.

So the distance is

61.06 ✗ 60 =3663 nautical miles.

Note: terrestrial coordinates are actually more complicated than this, because the Earth is not really a sphere. One source where you can find out more about this is the Ordnance Survey's: