حركة الشمس و ضبط الوقت

English المواضيع
positional

حركة الشمس و أثرها في ضبط الوقت

In the ecliptic system, the Sun's coordinates are fairly simple, because its ecliptic latitude is 0° at all times, while its ecliptic longitude constantly increases.

However, the Sun's longitude does not increase at a steady speed of exactly 360° a year. And it's important to know the Sun's position, because it's used for normal time-keeping (solar time, rather than sidereal time).

By Kepler's Second Law,
the Earth orbits faster at perihelion and slower at aphelion.
So the Sun appears to move fastest along ecliptic in January
and slowest in July. We can invent an imaginary Sun (the dynamical mean Sun)
which coincides with the true Sun when the Earth is at perihelion, but moves along the ecliptic at a constant speed.
The true Sun appears to move faster than the dynamical mean Sun when the Earth is around perihelion, and slower when the Earth is near aphelion: one cycle per year.

However, an object moving at a constant speed along the ecliptic
is still moving at a varying speed with respect to the equator,
since the ecliptic is tilted to the equator. We invent another imaginary Sun, called simply the mean Sun, which moves along the equator at constant speed; the dynamical mean Sun appears to lag behind this
where the ecliptic is steeply tilted to the equator (around the equinoxes)
and catch up where it's nearly parallel (around the solstices):
two cycles per year.

Combining these two effects gives the total difference in time between the true Sun and the mean Sun, which is called the equation of time (the solid black line on the diagram).

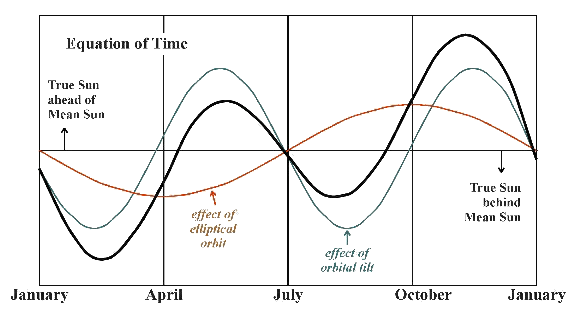
The true Sun is about 14 minutes late, compared to the mean Sun, around 10th February, about 4 minutes early around May 15th, about 6 minutes late around July 25th, and about 16 minutes early around November 5th.

The interval between two meridian transits of the mean Sun is the mean solar day. The upper transit of the mean Sun across the local meridian marks midday, local mean time. Greenwich Mean Time (GMT) is defined as midday when the mean Sun crosses the meridian of Greenwich.

Apparent solar time, as measured by the the true Sun (e.g. on a sundial), may differ from GMT for three reasons.
Firstly, because of the equation of time,
Secondly, because of the longitude of the observer (the further west, the later the Sun will cross the meridian).
Thirdly, because of "Summer Time".

Britain uses GMT as standard time in winter, adding one hour in summer. Most other countries adopt their own standard time,
suitable for their own longitude (large countries may have several time-zones), differing from GMT by a set amount.

In practice, the Earth's rotation is not quite constant. Time is now regulated by atomic clocks, and called Coordinated Universal Time (UTC), but this is artificially kept within 1 second of GMT
by adding a "leap second" when necessary.

Astronomers also use Terrestrial Time (TT, formerly called Ephemeris Time, ET)
for describing the motions of solar-system bodies.
The difference TT-UTC is called "delta-T".

At any location, local mean time and local sidereal time agree at the autumn equinox. (Why? Because, at the autumn equinox, the Right Ascension of the mean Sun is 12 hours,
and the mean Sun is on the local meridian at 12h, local mean time.) But sidereal time runs faster than solar time, by one day a year,
or approximately 3.94 minutes a day.

تمرين:

On April 1st, what is the Sun's approximate ecliptic longitude?
And approximately what is Greenwich Sidereal Time at midnight on April 1st?

الحل:

At the spring equinox, on or around March 21st,
the Sun's ecliptic longitude is exactly 0°. 11 days have elapsed since then, so the Sun's longitude will be approximately 11°.
(Only approximately,
because the ellipticity of the Earth's orbit means that the Sun does not move around the ecliptic at a steady speed.)

And approximately what is Greenwich Sidereal Time at midnight on April 1st?

GST and GMT are the same at the autumn equinox, so they are exactly 12 hours out of phase at the spring equinox. So GST is 12h at midnight on March 21st, approximately.

Eleven days later, on April 1st, GST will have got ahead of GMT by 11 x 3.94 minutes = 43.3 minutes. So GST at midnight on April 1st will be approximately 12h43m.

After this digression into the topic of time, we now return to the position of an object in the sky. There are various physical factors which may change the apparent position of an object.