الإحداثيات الأفقية

الإحداثيات الأفقية - نظام "alt-az"

إن موضع الأجرام على الكرة السماوية ثابت و محدد بإحداثيات سماوية مشابهة لتلك المواضع على الكرة الأرضية المحددة بإحداثيات طول\عرض.

يتوفر أنظمة إحداثيات مختلفة تستخدم لأغراض مختلفة ; كل نظام يحتاج إلى دائرة سماوية مرجعية و إلى نقطة ثابتة عليها.

النظام الإحداثي الأكثر بساطة هو النظام الأفقي, و الذي يستخدم أفق المكان كدائرة مرجعية له.

(الشكل-16) يختلف أفق المكان بحسب خط عرض الراصد

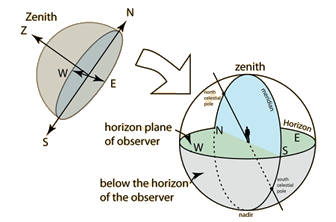
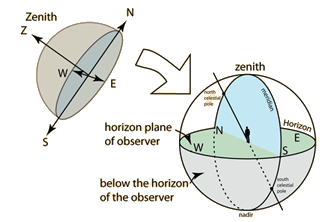
(الشكل-17) أفق المكان بحسب الراصد

و أما أقطاب هذه الدائرة فهي نقطتي السمت فوق رأس الراصد و نقطة النظير أسفل أقدام الراصد; و تحدد هاتين النقطتين محلياً بشكل خط شاقولي يشكل محور القبة .

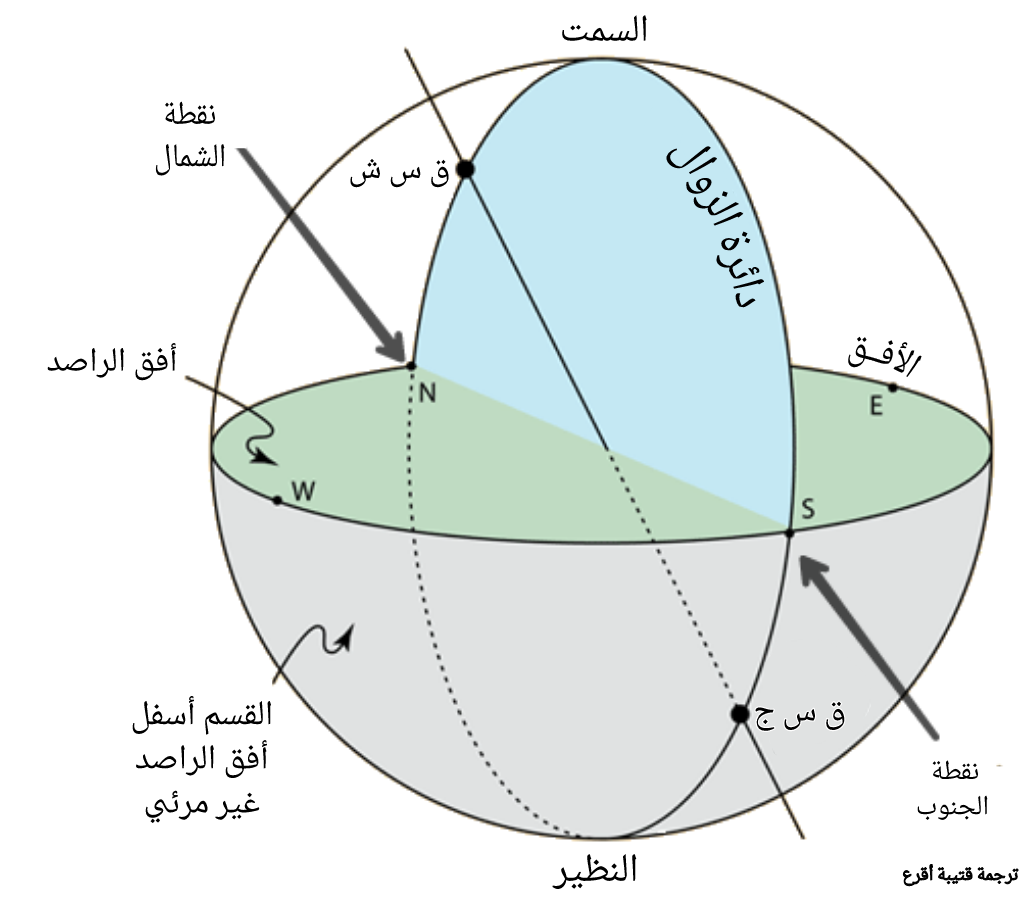
(الشكل-18) السمت و النظير و أفق المكان و دائرة الزوال

قم برسم دائرة شاقولية من نقطة السمت إلى النظير و مارة بالنقطة X.

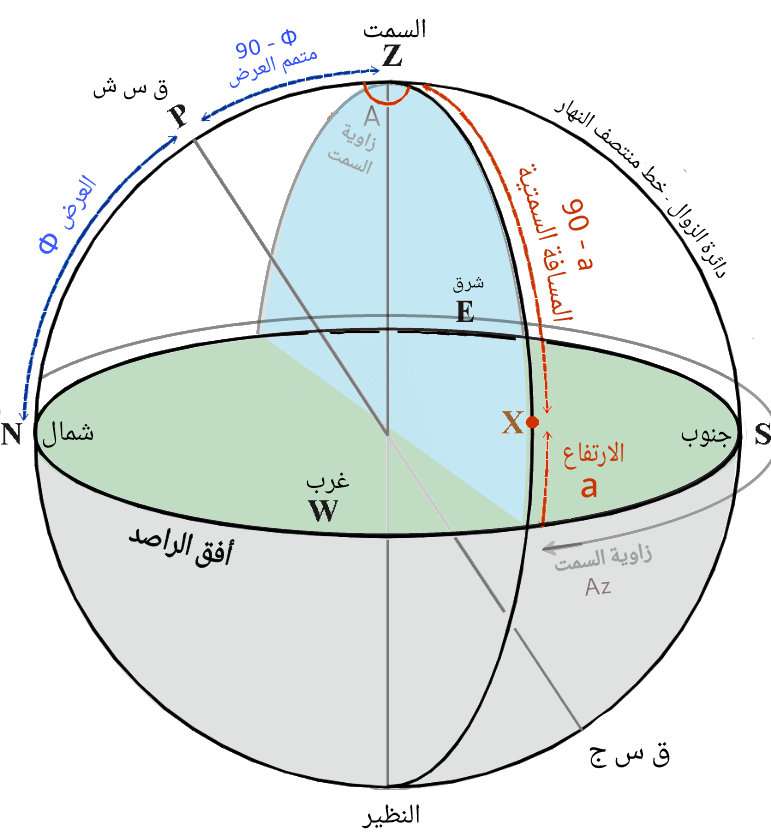(الشكل-19) عناصر الاحداثيات الافقية

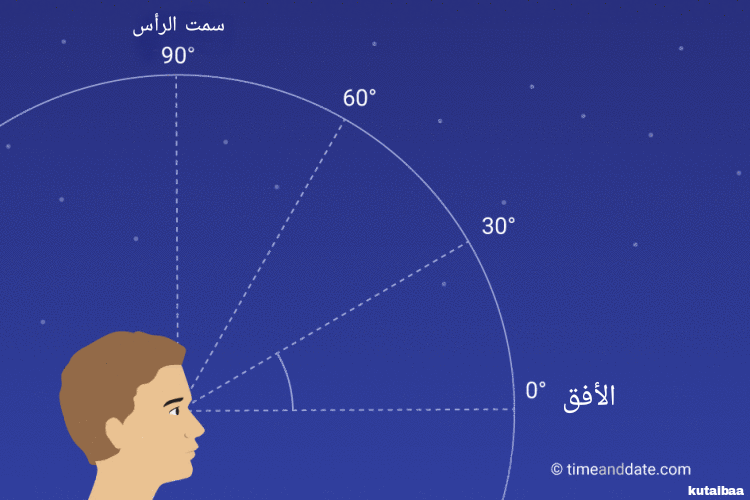
إن الارتفاع (a) للنقطة X هو المسافة الزاوية بين دائرة الأفق و الممثلة بالقوس الشاقولي النازل من النقطة x باتجاه دائرة الأفق. و تقاس بقيم ما بين -90° عند نقطة النظير و حتى +90° لنقطة سمت الرأس. و كقيمة بديلة يستخدم , البعد السمتي للنقطة X و هي تساوي 90° - a.

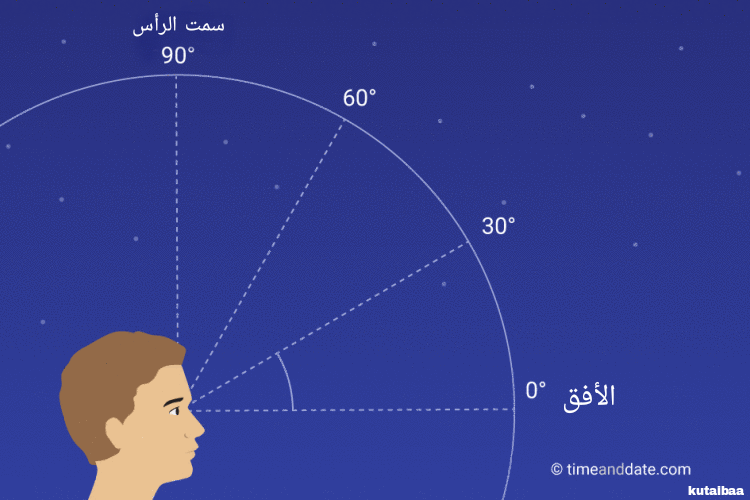(الشكل-20) قياس ارتفاع الأجرام السماوية من الأفق إلى سمت الرأس

(يستخدم البعض الرمز h بدلاً من a .)

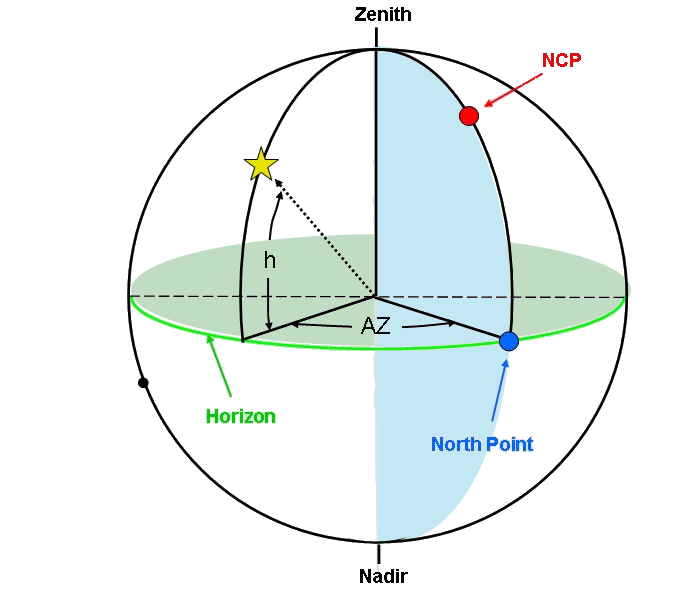
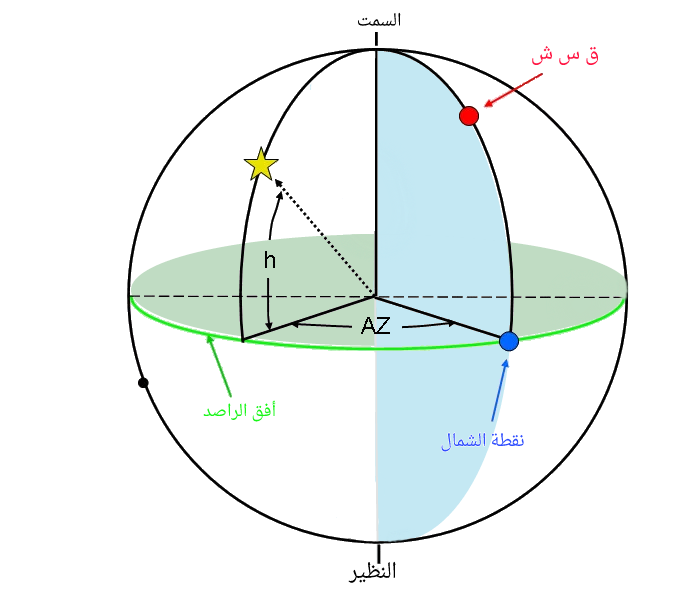(الشكل-21) استخدام الرمز البديل لقيمة احداثي الارتفاع

إن أي جرمين يملكان قيمة الارتفاع نفسها يقعان على دائرة واحدة تدعى موازي الارتفاع.

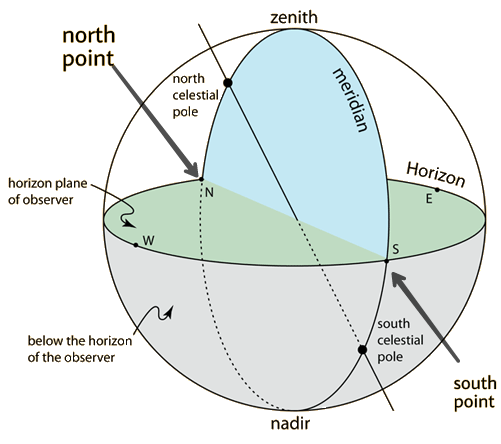
و لتحديد نقطة مرجعية على دائرة الأفق نبحث عن مكان تقاطع المحور الدوراني للأرض مع قبة السماء, و هو اتجاه القطب الشمالي و القطب الجنوبي. الدائرة الشاقولية المارة بهاتين النقطتين ندعوها دائرة الزوال. و عند تقاطعها مع الأفق فإنها تحدد لنا نقطتي الشمال و الجنوب على دائرة الأفق.

(الشكل-18) تعاريف خاصة بالإحداثيات الأفقية

أي نقاط الاتجاهات (نقطة الشمال هي تلك النقطة القريبة من القطب السماوي الشمالي). و في منتصف المسافة بين كلا الاتجاهين تقع نقطتي الشرق و الغرب وتسمى الدائرة الشاقولية التي تتعامد مع دائرة الزوال والتي تمر من نقطتي الشرق والغرب الدائرة الشاقولية الأولى (ليست ظاهرة في الرسم ), و تشكل 90° مع دائرة الزوال .

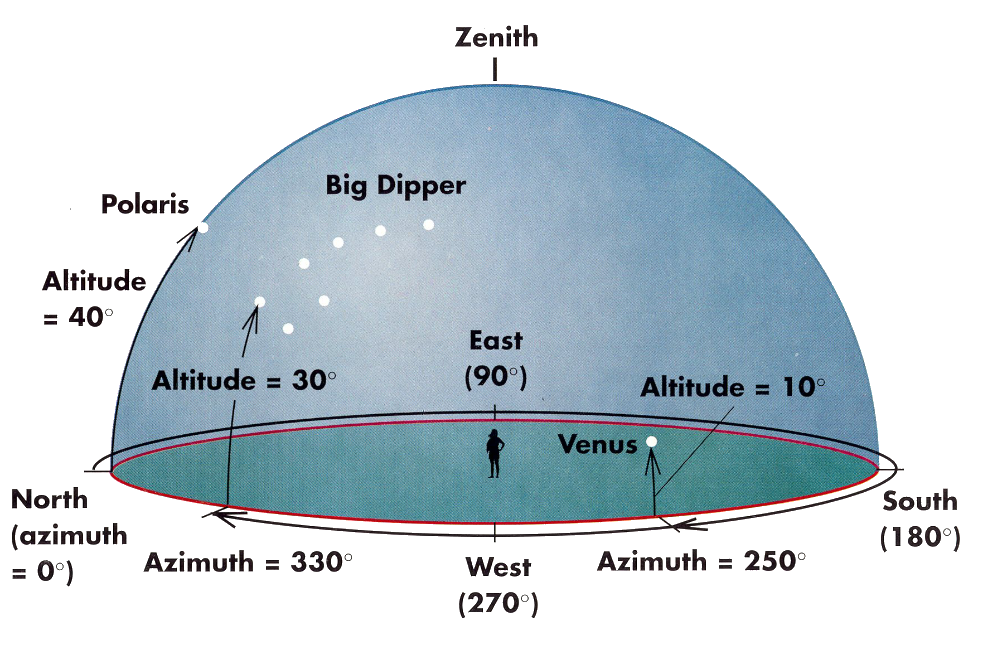
تعرف الزاوية السمتية (Az) لنقطة X بالمسافة الزاوية حول الأفق من نقطة الشمال إلى الدائرة الشاقولية المارة بالجرم x , و يقاس من القيمة 0° و حتى 360° مع اتجاه دوران عقارب الساعة. لاحظ كوكب الزهرة و أحد نجوم الدب الأكبر في الشكل التالي و تعرف على إحداثياتها الأفقية.

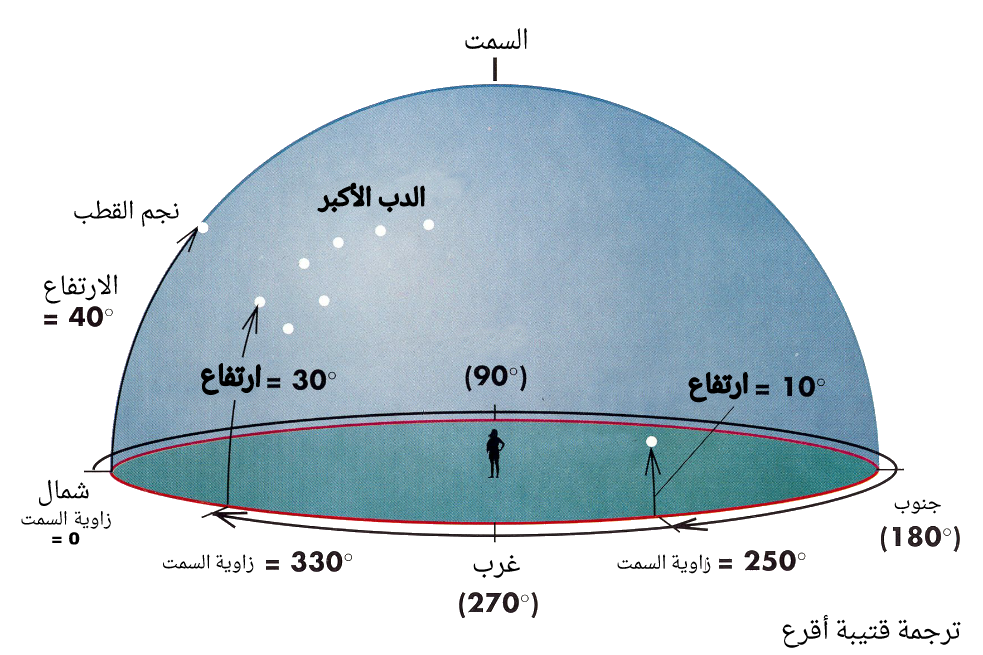(الشكل-22) تعريف الزاوية السمتية و الارتفاع لعدة أجرام سماوية مثل الزهرة و نجم القطب

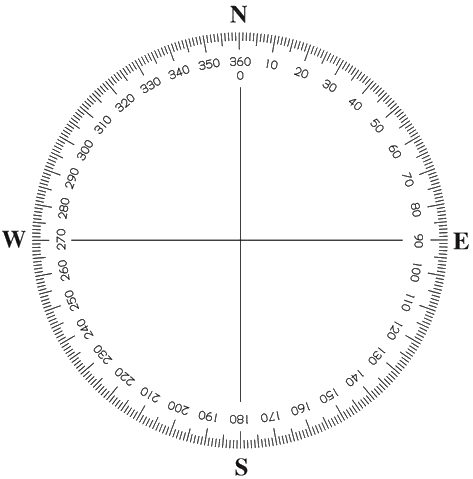
و هذه دائرة الأفق بحسب التقسيم المتداول لحساب الزاوية الساعية التي تكلمنا عنها

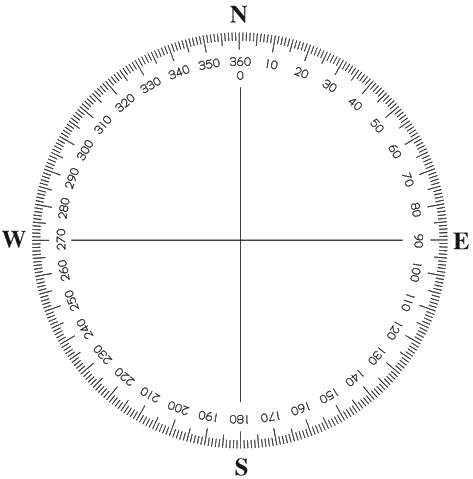(الشكل-23) نقاط الاتجاهات الاربعة و التقسيم المتداول لحساب الزاوية الساعية

تذكر بأن ارتفاع نقطة القطب الشمالي يساوي تماماً العرض لموقع الراصد على سطح الأرض . و ذلك موضح بالشكل التالي حيث يقع الراصد على خط عرض 40 درجة

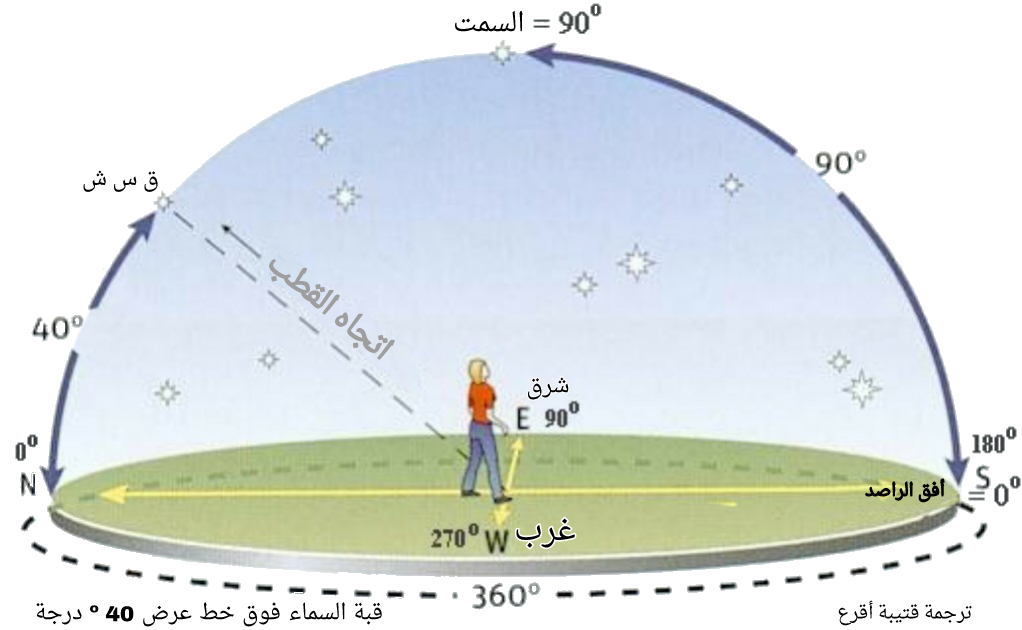(الشكل-24) ارتفاع نقطة القطب و التقسيم المتداول لحساب الزاوية الساعية

و هذه مقارنة بين الإحداثيات الأفقية و نظام الإحداثيات الجغرافي الأرضي :

أرضية جغرافية	أفقية سماوية alt-az
دائرة الاستواء	دائرة الأفق
القطب الشمالي	نقطة السمت
القطب الجنوبي	نقطة النظير
عرض	ارتفاع
البعد القطبي	البعد السمتي
دائرة موازي العرض	دائرة موازي الارتفاع
دائرة زوال الطول	الدائرة الشاقولية
خط زوال غرينتش	دائرة الزوال
طول	زاوية سمتية

تمرين:

From St.Andrews, at 6 pm on 1998 February 2nd, the Moon appeared at

الارتفاع +39°, زاوية السمت 196°

, while Saturn was at

الارتفاع +34°, زاوية السمت 210°

How far apart did the two objects appear? Which was further east?

الحل

(الشكل-24) المثلث الكروي حسب معطيات المسألة

The difference in azimuth is 14°.

Use the cosine rule:

cos MS = cos MZ cos ZS + sin MZ sin ZS cos Z
cos MS = 0.98
so
MS = 12.3°

Which was further east?

The Moon is further east, and higher up, than Saturn.

Horizontal Coordinates

Arabic Index

Horizontal "alt-az" Coordinate System

The location of an object on the sky is fixed by celestial coordinates analogous to the terrestrial latitude/longitude system.

There are various systems, suitable for different purposes; each system needs a fundamental circle and a fixed point on it.

The simplest is the horizontal system, which uses the horizon as its fundamental circle.

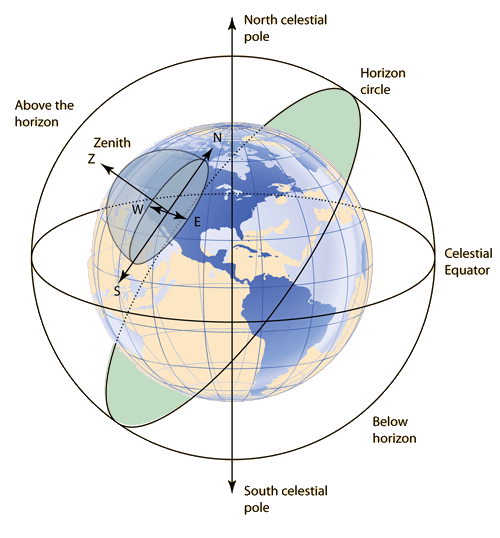(Figure-16) Horizon determined relative to observer latitude

(Figure-17) Observer Horizon

The poles of this circle are the zenith overhead and the nadir underfoot; these are defined by the local vertical (using a plumb-line or similar).

(Figure-18) Defining horizontal elements

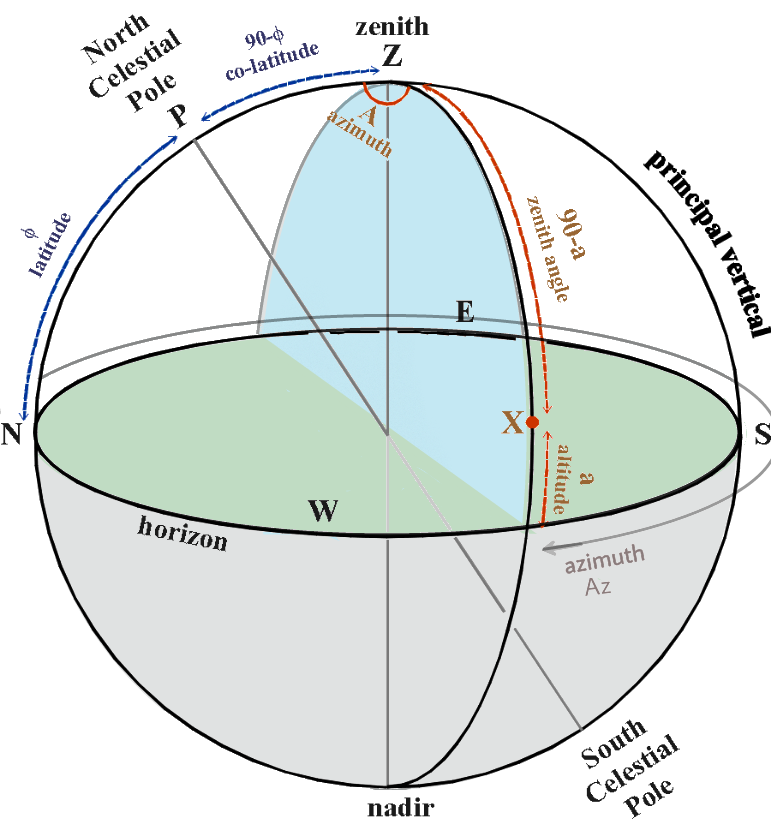Draw a vertical circle from the zenith to the nadir through object X.

(Figure-19) Elements of the horizontal coordinates

The altitude (a) of object X is the angular distance along the vertical circle from the horizon to X, measured from -90° at nadir to +90° at zenith. Alternatively, the zenith distance of X is 90° - a.

(Figure-20) Measuring altitude from horizon to azimuth point

(Some authors use h instead of a .)

(Figure-21) using ' h ' instead of ' a '

Any two objects with the same altitude lie on a small circle called a parallel of altitude.

To fix a point of origin on horizon,
we look at where the spin axis of the Earth intersects the celestial sphere, at the North and South Celestial Poles. The vertical circle through these is called the principal vertical. Where this intersects the horizon, it gives the north and south cardinal points (the north point is the one nearest the North Celestial Pole). Midway between these are the east and west cardinal points; the vertical circle through these is called the prime vertical(not shown on the diagram), at 90° to the principal vertical.

The azimuth (A) of object X is the angular distance around the horizon from the north cardinal point to the vertical circle through X, measured 0°-360° westwards (clockwise).

(Figure-22) Altitude and Azimuth for many celestial objects

(Figure-23) cardinal points division of the horizon circle

Note that the altitude of the North Celestial Pole is equal to the latitude of the observer.

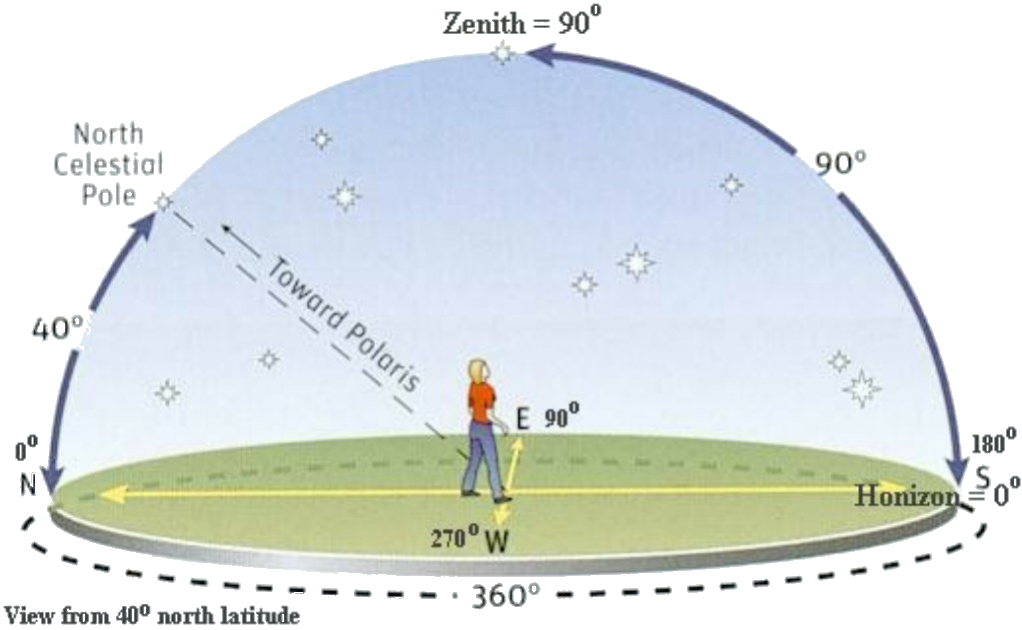(Figure-24) altitude of celestial pole depends on observer latitude

Comparison with the terrestrial system:

Terrestrial	Celestial "alt-az"
equator	horizon
North Pole	zenith
South Pole	nadir
latitude	altitude
co-latitude	zenith distance
parallel of latitude	parallel of altitude
meridian of longitude	vertical circle
Greenwich Meridian	Principal Vertical
longitude	azimuth

Exercise:

From St.Andrews, at 6 pm on 1998 February 2nd, the Moon appeared at

altitude +39°, azimuth 196°

, while Saturn was at

altitude +34°, azimuth 210°

How far apart did the two objects appear? Which was further east?

Answer

(Figure-24) Spherical triangle as is.