• "الفلك الموضعي"

• مقدمة
• الكرة الأرضية
• هندسة المثلثات الكروية
• ملاحظات حول الهندسة الكروية
• إحداثيات أفقية "alt-az"
• إحداثيات استوائية "HA-dec"
• إحداثيات استوائية "RA-dec"
• الزمن النجمي
• الانتقال بين أفقي و استوائي
• إحداثيات مجرية
• إحداثيات بروجية
• الانتقال بين بروجي و استوائي
• حركة الشمس و ضبط الوقت
• القمر
• الإنكسار الجوي
• شروق و غروب الشمس، الشفق
• اختلاف المنظر المركزي اليومي
• اختلاف المنظر الموسمي
• الزيغ
• المبادرة و الترنح :اضطراب محور الأرض
• تقاويم
• الامتحان الأخير
• الإحداثيات الفلكية، خضر الأحمد
• الحركة الظاهرية للنجوم (تفاعلي)
• الأقطاب السماوية (تفاعلي)

الهندسة الكروية

الهندسة الكروية

يناظر قوس الدائرة الكبرى على سطح الكرة و يماثل الخط المستقيم في المستوي.

و بتقاطع اثنين من هذه الأقواس, نستطيع تعريف الزاوية الكروية و كذلكالزاوية بين مماسي القوسين عند نقطة التقاطع, أو الزاوية بين مستويي الدائرتين الكبيرتين عند تقاطعهما في مركز الكرة. (تعرف الزاوية الكروية فقط في نقاط التقاء أقواس الدوائر الكبيرة .)

يتألف المثلث الكروي من ثلاثة أقواس لدوائر كبرى, مجموعها كلها أقل من 180°. إن مجموع الزوايا غير ثابت, و لكنه دائماً هو أكبر من 180°. و يدعى المثلث الذي يمتلك قيمة 90° لأحدى زواياه; quadrantal.

(الشكل-9) المثلث الكروي

يوجد العديد من الصيغ الرياضية المتعلقة بزوايا و أطراف المثلث الكروي. و سوف نستخدم في هذا الكورس صيغتين فقط : صيغة الجيب و جيب التمام.

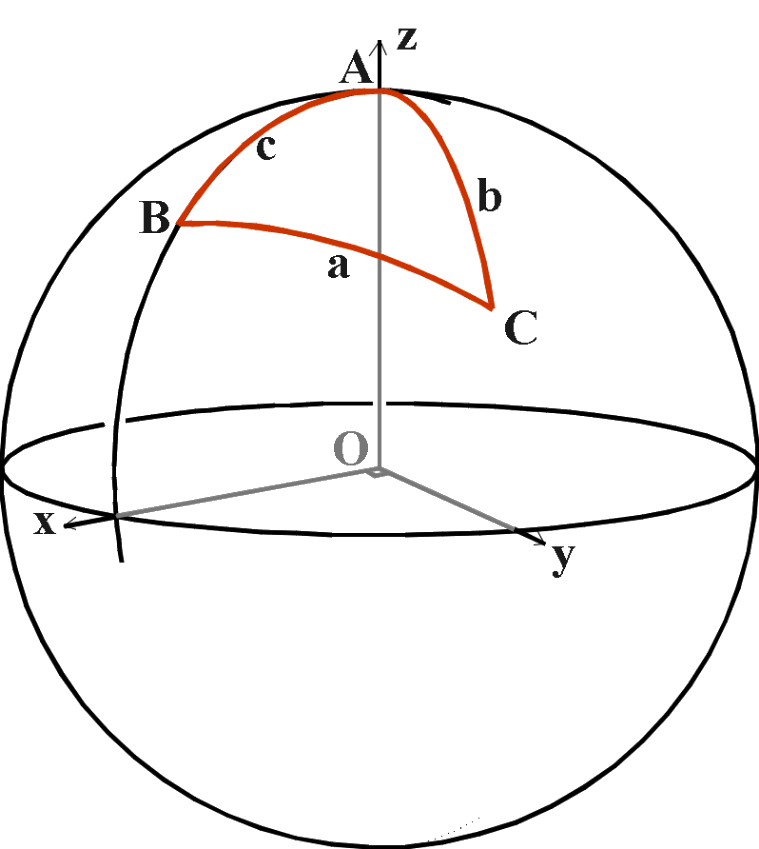(الشكل-10) المثلث الكروي في إحداثيات XYZ

سنفترض المثلث ABC على سطح كرة قطرها = 1.

(See ملاحظات حول الهندسة الكروية)

نستخدم الحروف الكبيرة A, B, C للإشارة إلى الزوايا ; في الوقت الذي تستخدم رموز الأحرف الصغيرة a, b, c للإشارة إلى الأقواس المقابلة للزوايا. (تذكر دائماً, إن أطراف المثلث في الهندسة الكروية هي أقواس دوائر كبرى, و بالتالي فهي أيضاً تعتبر زوايا.)

قم بتدوير الكرة بحيث تضع النقطة A عند "القطب الشمالي", و سوف نعتبر القوس AB تعريفاً "للزوال الرئيسي".

نفترض الآن نظام إحداثيات متعامد OXYZ: حيث تقع O في مركز الكرة; و يمر الخط OZ عبر النقطة A; المستوي OX يمر عبر القوس AB (أو عبر امتداده); المستوي OY معامد لكلا المستويين السابقين. و في نظامنا الإحداثي هذا فإن إحداثيات النقطة C :

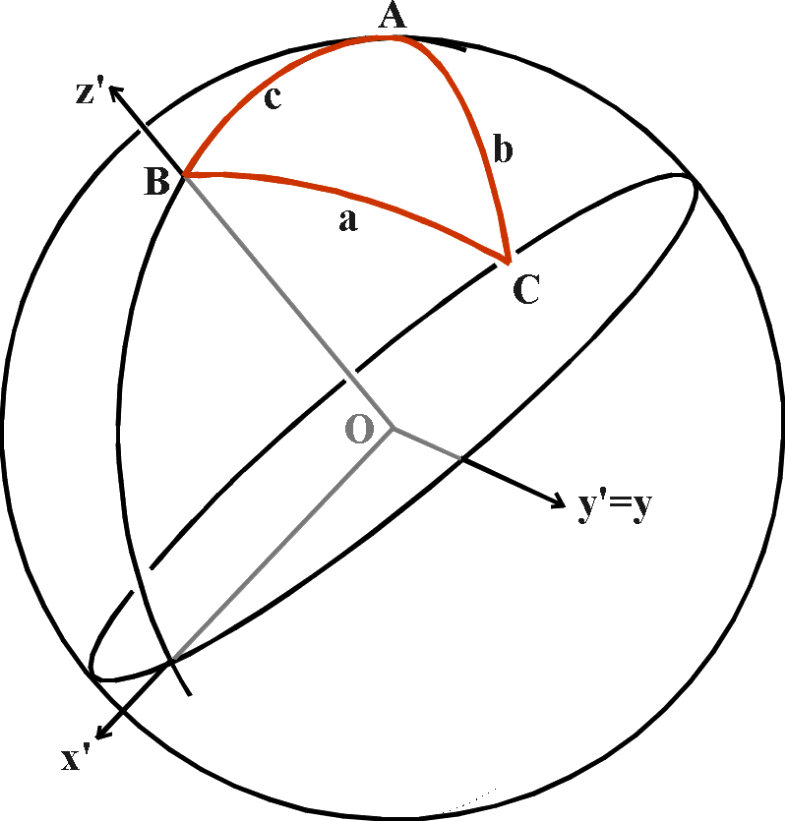(الشكل-11) المثلث الكروي في إحداثيات جديدة بعد عملية الدوران

و الآن لنقم بإنشاء مجموعة إحداثية جديدة, مع ترك المحور y ثابتاً و تحريك "القطب" من النقطة A إلى النقطة B ( بما يعني تدوير المستوي x,yعبر الزاوية c). و تكون الإحداثيات الجديدة ل C هي كالتالي:

و ببساطة فإن العلاقة بين الإحداثيات القديمة و الجديدة هي دوران للمحاور x,z عبر الزاوية c :

و بالتالي نحصل على الصيغ التالية :

هذه المعادلات تعطينا الصيغ القادرة على حل المثلثات الكروية.

المعادلة الأولى هي قانون جيب التمام المعدل, و الذي يكون مفيداً في بعض الحالات و لكن لا يطلب تذكره و حفظه

المعادلة الثانية تبرز قانون الجيب. و يمكن ترتيب هذه المعادلات كالتالي :

بشكل مشابه,

عادة ما يكتب قانون الجيب بالشكل التالي:

المعادلة الثالثة تعطينا قانون جيب التمام:

و بشكل مشابه نكتب:

و هنا القوانين الثلاثة بشكل نهائي:

يستطيع قانون جيب التمام تقريباً حل مجمل مسائل المثلث الكروي إذا استخدمت بشكل كاف. أما قانون الجيب فحفظه أسهل لكنه غير كاف في العديد من المسائل.

تذكربأن كلا الصيغتين ربما تعانيان من الالتباس في النتائج :

و على سبيل المثالإن كانت نتيجة قانون الجيب

فيمكن ل x أن تكون 30° أو 150° !!.

و ربما نتج عن قانون جيب التمام

عندها تكون قيمة الزاوية x هي 60° أو ربما 300° (-60°). في هذه الحالة لا يكون هناك التباس إن كانت x هي القوس في المثلث, و هو ما يعني أن قيمته أقل من 180°, لكن ربما سيكون هناك شيء من الشك فيما لو كانت قيمة الزاوية للمثلث ذات قيمة موجبة أو سالبة.

لهذه الأسباب, عند تطبيق أي من هذه الصيغ, تأكد من كون النتائج ذات معنى منطقي.و في حال الشك, قم باستخدام صيغ أخرى للتأكد من النتيجة.

تمرين:

مدينة Alderney, في جزر الشانيل ذات إحداثيات

طول 2°W, عرض 50°N

مدينة Winnipeg, الكندية, ذات إحداثياتhas

طول 97°W, عرض 50°N

ما هو البعد بين المدينتين محسوباً بالميل البحري, على طول قوس الدائرة الكبرى؟

إن أردت رسم طريق من مدينة Alderney على الدائرة الكبرى باتجاه مدينة Winnipeg, ففي أي اتجاه عليك التوجه (المقصود باتجاه أي سمت)؟

الحل

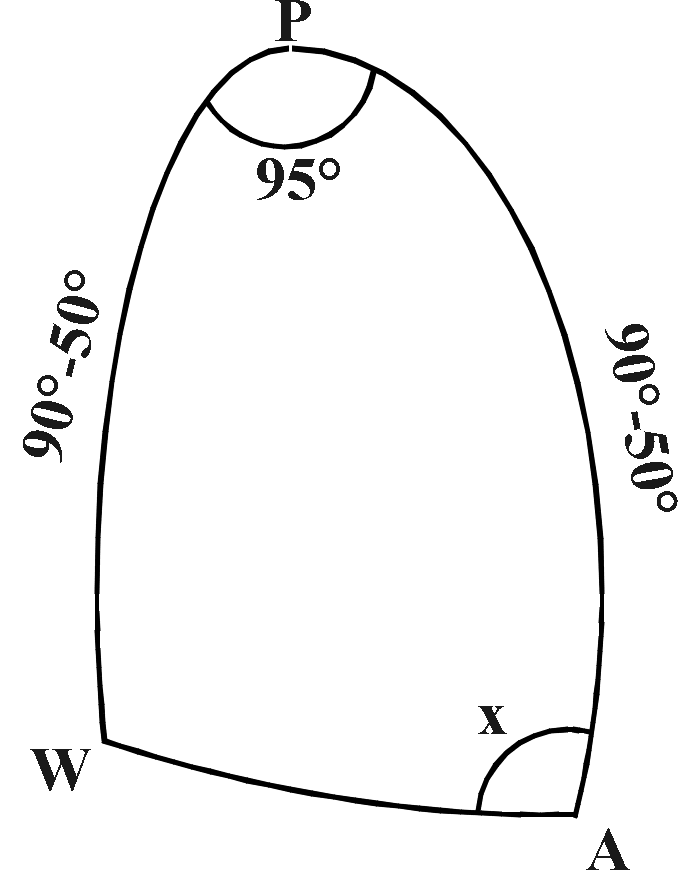(الشكل-12) المثلث بحسب معطيات التمرين

p تمثل نقطة القطب الشمالي , و A تمثل مدينة Alderney ,أما w فتمثل مدينة winnipeg. لنستخدم قانون جيب التمام :

cos AW = cos WP cos AP + sin WP sin AP cos P
= cos²40° + sin²40° cos 95°
= 0.5508
بالتالي طول القوس يساوي
AW = 56.58°
= 3395 nautical miles

(هذه القيمة أقل 7% من المسار على دائرة العرض الموازي ).

إن أردت رسم طريق من مدينة Alderney على الدائرة الكبرى باتجاه مدينة Winnipeg, ففي أي اتجاه عليك التوجه (المقصود باتجاه أي سمت)؟

سنستخدم قانون الجيب :

sin A / sin WP = sin P / sin WA
بالتالي
sin x = sin 40° sin 95° / sin 56.58° = 0.77
بالتالي

x = 50.1° or 129.9° .

و الاحساس يقودنا إلى 50.1° (أو يمكنك استخدام قانون جيب التمام للقوس PW).
يقاس السمت باتجاه عقارب الساعة بدءاً من الشمال, بالتالي فإن السمت
360° - 50.1° = 309.9° وهو السمت الذي تقع عليه مدينة winnipeg في أفق مدينة alderney. من الواضح انه باتجاه الشمال الغربي.

• "Positional Astronomy"

• Introduction
• the Terrestrial Sphere
• Spherical Trigonometry
• Notes on Spherical Trigonometry
• Horizontal Coordinates "alt-az"
• Equatorial system "HA-dec"
• Equatorial system "RA-dec"
• Sidereal Time
• Conversions: horizontal & equatorial
• Galactic coordinates
• Ecliptic coordinates
• Relation between ecliptic and equatorial
• Sun's motiont&time-keeping
• The Moon
• Refraction
• Sunrise, sunset, twilight
• Geocentric or diurnal parallax
• Annual parallax
• Aberration
• Precession
• Calendars
• Final Exercise
• Celestial Coordinates (arabic)
• Interactive Apparent Stars Motions
• Interactive Celestial Poles

Spherical Trigonometry

Spherical Trigonometry

A great-circle arc, on the sphere, is the analogue of a straight line, on the plane.

Where two such arcs intersect, we can define the spherical angle either as angle between the tangents to the two arcs, at the point of intersection, or as the angle between the planes of the two great circles where they intersect at the centre of the sphere. (Spherical angle is only defined where arcs of great circles meet.)

(Figure-9) Spherical Triangle

A Spherical Triangle is made up of three arcs of great circles, all less than 180°. The sum of the angles is not fixed, but will always be greater than 180°. If any side of the triangle is exactly 90°, the triangle is called quadrantal.

There are many formulae relating the sides and angles of a spherical triangle. In this course we use only two: the sine rule and the cosine rule.

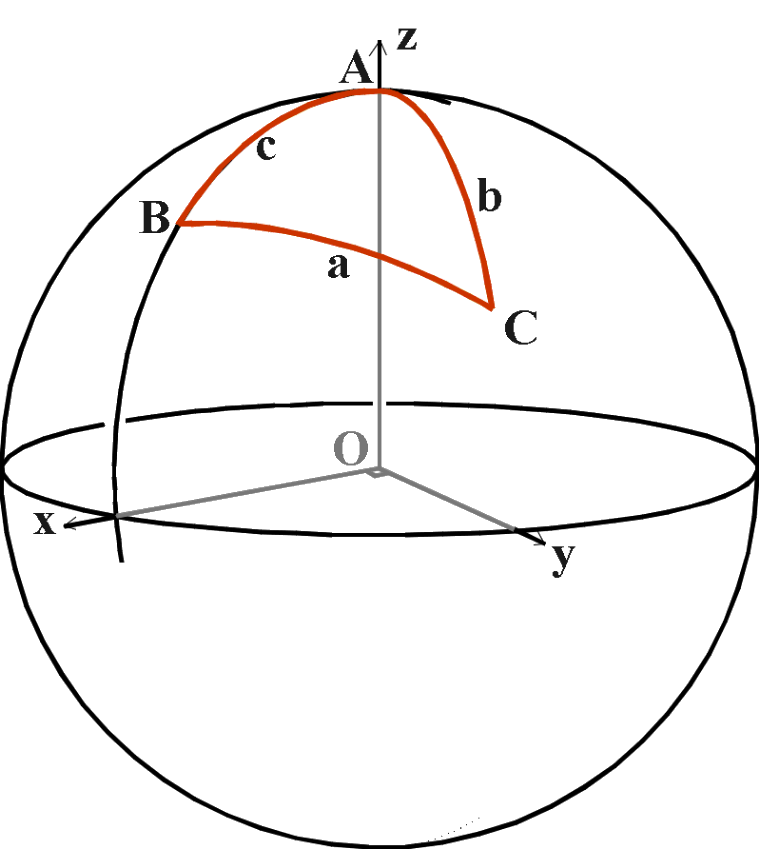(Figure-10)

Consider a triangle ABC on the surface of a sphere with radius = 1.

(See Notes on Spherical Trigonometry)

We use the capital letters A, B, C to denote the angles at these corners;
we use the lower-case letters a, b, c to denote the opposite sides.
(Remember that, in spherical geometry, the side of a triangle is the arc of a great circle, so it is also an angle.)

Turn the sphere so that A is at the "north pole",
and let arc AB define the "prime meridian".

Set up a system of rectangular axes OXYZ: O is at the centre of the sphere; OZ passes through A; OX passes through arc AB (or the extension of it); OY is perpendicular to both.
Find the coordinates of C in this system:

(Figure-11)

Now create a new set of axes, keeping the y-axis fixed and moving the "pole" from A to B (i.e. rotating the x,y-plane through angle c).
The new coordinates of C are

The relation between the old and new systems
is simply a rotation of the x,z-axes through angle c:

That is:

These three equations give us the formulae for solving spherical triangles.

The first equation is the transposed cosine rule, which is sometimes useful but need not be memorised.

The second equation gives the sine rule. Rearrange as:

Similarly,

So the sine rule is usually expressed as:

The third equation gives the cosine rule:

and similarly:

Here they are together:

The cosine rule will solve almost any triangle if it is applied often enough.
The sine rule is simpler to remember but not always applicable.

Note that both formulae can suffer from ambiguity:
E.g. if the sine rule yields
sin(x) = 0.5, then x may be 30° or 150°.
Or, if the cosine rule yields
cos(x) = 0.5, then x may be 60° or 300° (-60°).
In this case, there is no ambiguity if x is a side of the triangle, as it must be less than 180°, but there could still be uncertainty if an angle of the triangle was positive or negative.

So, when applying either formula, check to see if the answer is sensible. If in doubt, recalculate using the other formula, as a check.

Exercise:

Alderney, in the Channel Islands, has

longitude 2°W, latitude 50°N

Winnipeg, in Canada, has

longitude 97°W, latitude 50°N

How far apart are they, in nautical miles, along a great-circle arc?

If you set off from Alderney on a great-circle route to Winnipeg, in what direction (towards what azimuth) would you head?

Answer

(Figure-12)

Use the cosine rule:

cos AW =
cos WP cos AP + sin WP sin AP cos P
= cos²40° + sin²40° cos 95°
= 0.5508
So AW = 56.58°
= 3395 nautical miles

(This is 7% shorter than the route along a parallel of latitude).

If you set off from Alderney on a great-circle route to Winnipeg,
in what direction (towards what azimuth) would you head?

Use the sine rule:

sin A / sin WP = sin P / sin WA
so
sin x = sin 40° sin 95° / sin 56.58° = 0.77
so

x = 50.1° or 129.9° .

Common sense says 50.1° (or check using cosine rule to get PW).
Azimuth is measured clockwise from north, so azimuth is 360° - 50.1° = 309.9°

(Note that this is 40° north of the “obvious” due-west course.)