-
"الفلك الموضعي"
- مقدمة
- الكرة الأرضية
- هندسة المثلثات الكروية
- ملاحظات حول الهندسة الكروية
- إحداثيات أفقية "alt-az"
- إحداثيات استوائية "HA-dec"
- إحداثيات استوائية "RA-dec"
- الزمن النجمي
- الانتقال بين أفقي و استوائي
- إحداثيات مجرية
- إحداثيات بروجية
- الانتقال بين بروجي و استوائي
- حركة الشمس و ضبط الوقت
- القمر
- الإنكسار الجوي
- شروق و غروب الشمس، الشفق
- اختلاف المنظر المركزي اليومي
- اختلاف المنظر الموسمي
- الزيغ
- المبادرة و الترنح :اضطراب محور الأرض
- تقاويم
- الامتحان الأخير
- الإحداثيات الفلكية، خضر الأحمد
- الحركة الظاهرية للنجوم (تفاعلي)
- الأقطاب السماوية (تفاعلي)

إحداثيات استوائية (2) RA-Dec
{Note: If your browser does not distinguish between "a,b" and " α, β " (the Greek letters "alpha, beta") then I am afraid you will not be able to make much sense of the equations on this page.}
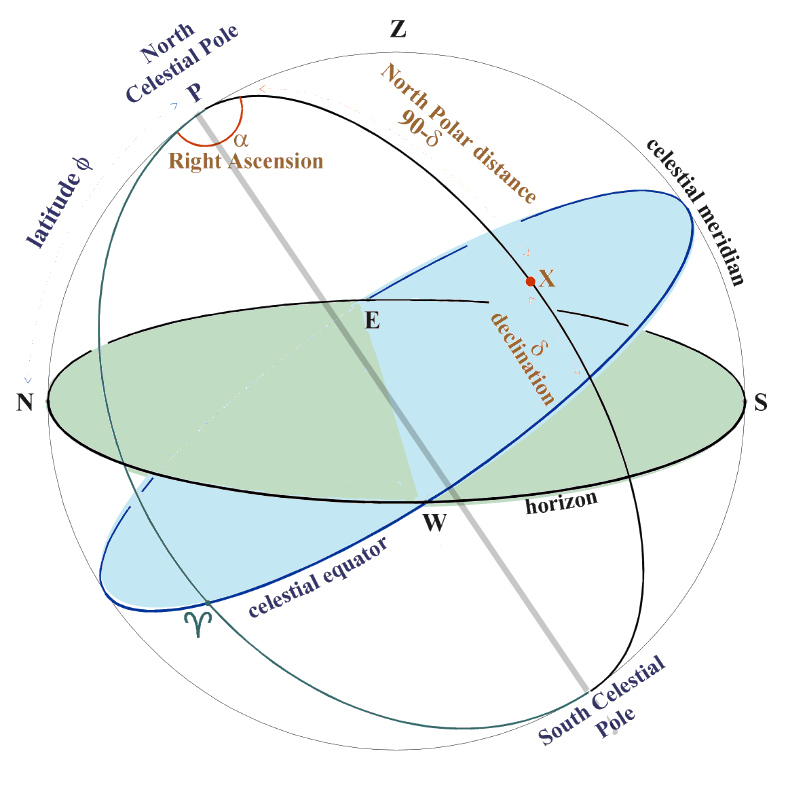
Coordinates
in the first equatorial system (HA and declination)
still depend
on the time of observation.
Now we change the zero-point
for our coordinates.
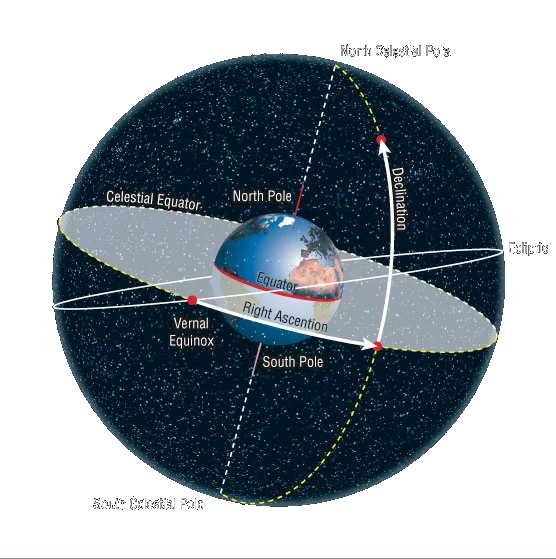
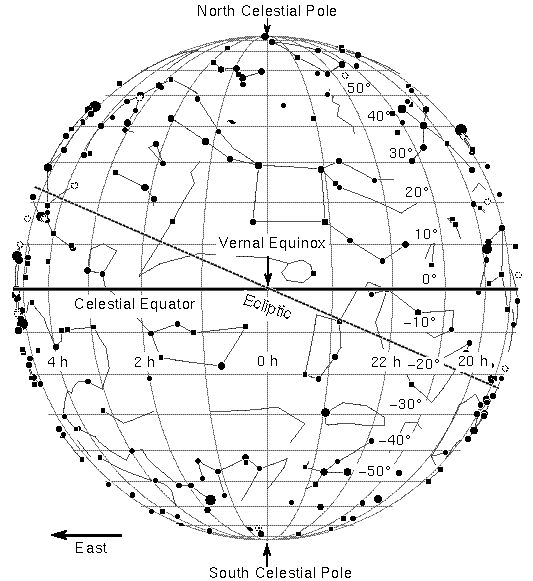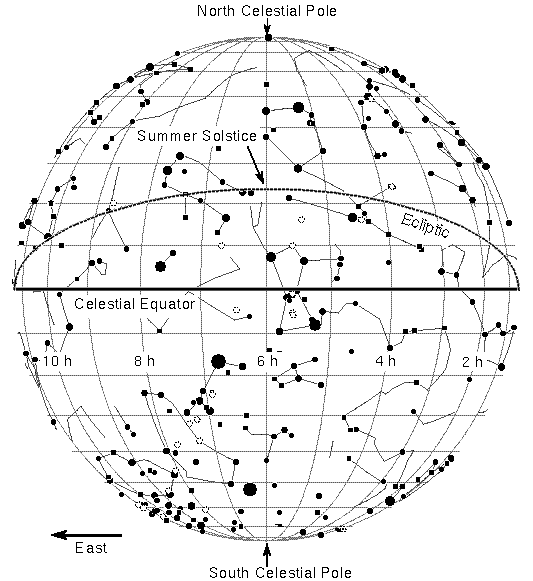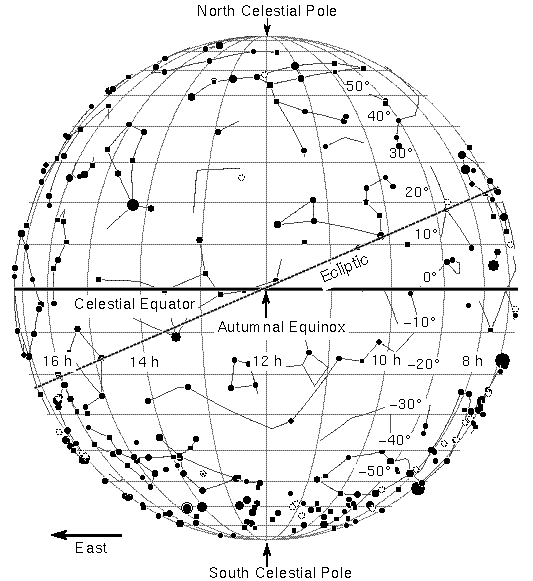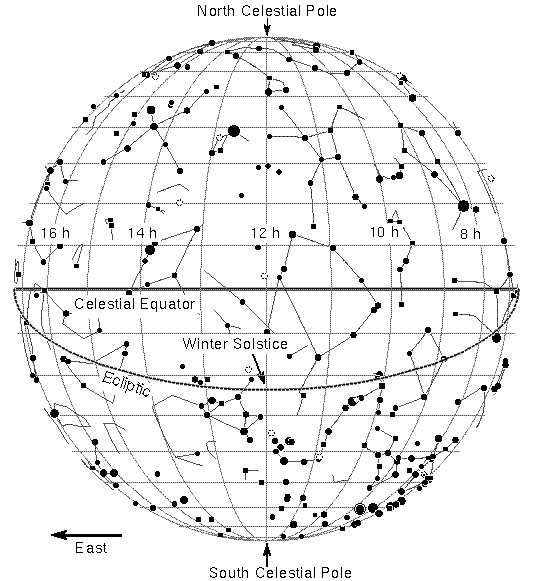
We choose a fixed point on the celestial
equator,
called the vernal equinox, or the First Point
of Aries.
The symbol for this is the astrological symbol for
Aries:

(The function of this point will become clearer later on.)
The declination
(δ) of object X is measured in the same way as before.
The
Right
Ascension or RA (α) of object X
is the angle along the celestial equator measured eastwards
from
the vernal equinox to the meridian of X.
Like HA, RA is measured
in hours 0-24h, but it goes in the opposite direction.
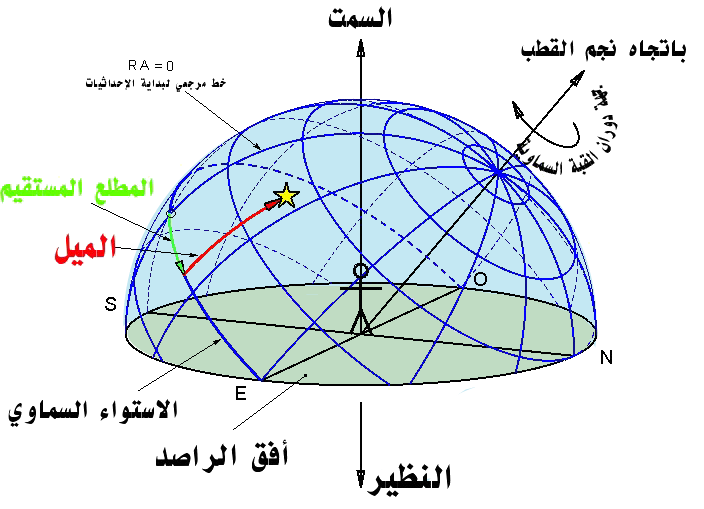
Comparison of these celestial coordinate systems with the terrestrial system:
| terrestrial | alt-az | HA-dec | RA-dec |
| equator | horizon | celestial equator | celestial equator |
| North Pole | zenith | North Celestial Pole | North Celestial Pole |
| South Pole | nadir | South Celestial Pole | South Celestial Pole |
| latitude | altitude | declination | declination |
| co-latitude | zenith distance | North Polar Distance | North Polar Distance |
| parallel of latitude | parallel of altitude | parallel of declination | parallel of declination |
| meridian of longitude | vertical circle | meridian | meridian |
| Greenwich Meridian | Principal Vertical | celestial meridian | vernal equinox |
| longitude | azimuth | Hour Angle | Right Ascension |
تمرين:
The four stars at the corners of the “Great Square of Pegasus” are:
|
star |
R.A. |
declination |
|
α And |
00h 08m |
+29°05' |
|
β Peg |
23h 04m |
+28° 05' |
|
α Peg |
23h 05m |
+15° 12' |
|
γ Peg |
00h 13m |
+15° 11' |
Calculate the lengths of the two diagonals of the “Square”.
الحل
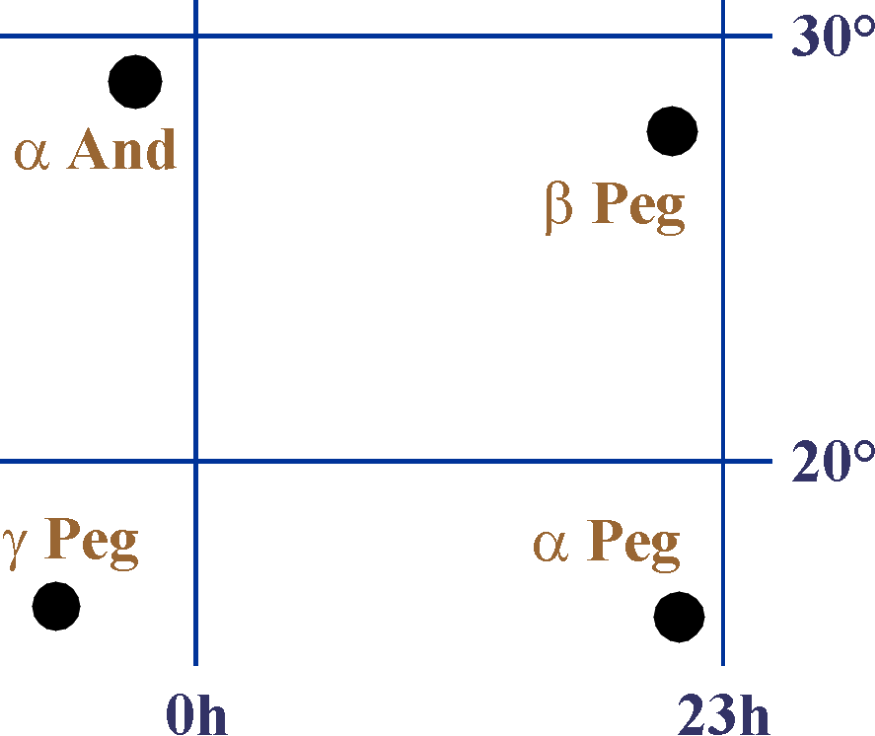
It is necessary to plot the
four stars, at least approximately,
to find out which pairs form
the diagonals!
Then, to find the length of
each diagonal, use the cosine rule:
cos S1S2
= cos S1P cos S2P + sin S1P sin S2P
cos P
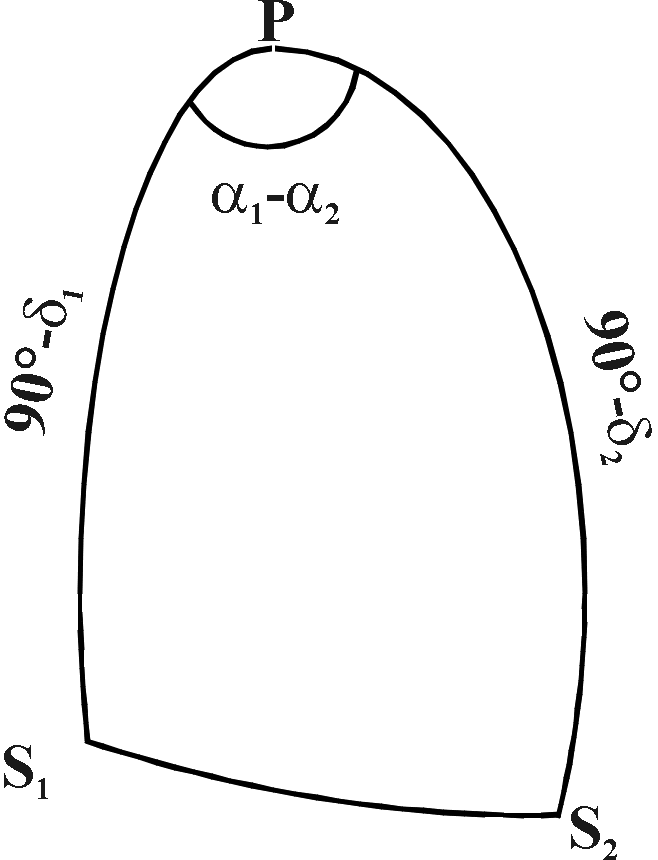
This gives {α And} to {α Peg} = 20.1°
and {β
Peg} to {γ Peg} = 20.5°.
The Right Ascension and declination of a star do not normally change over short periods of time; but the Hour Angle changes constantly with time. Consequently we have to find a way of defining the time.
- إحداثيات استوائية (1)
-
ترجمة قتيبة أقرع
- الزمن النجمي