-
"الفلك الموضعي"
- مقدمة
- الكرة الأرضية
- هندسة المثلثات الكروية
- ملاحظات حول الهندسة الكروية
- إحداثيات أفقية "alt-az"
- إحداثيات استوائية "HA-dec"
- إحداثيات استوائية "RA-dec"
- الزمن النجمي
- الانتقال بين أفقي و استوائي
- إحداثيات مجرية
- إحداثيات بروجية
- الانتقال بين بروجي و استوائي
- حركة الشمس و ضبط الوقت
- القمر
- الإنكسار الجوي
- شروق و غروب الشمس، الشفق
- اختلاف المنظر المركزي اليومي
- اختلاف المنظر الموسمي
- الزيغ
- المبادرة و الترنح :اضطراب محور الأرض
- تقاويم
- الامتحان الأخير
- الإحداثيات الفلكية، خضر الأحمد
- الحركة الظاهرية للنجوم (تفاعلي)
- الأقطاب السماوية (تفاعلي)

الاحداثيات البروجية
{Note: If your browser does not distinguish between "a,b" and "α, β" (the Greek letters "alpha, beta") then I am afraid you will not be able to make much sense of the equations on this page.}
All the objects considered so far have been "fixed stars", which keep almost constant values of Right Ascension and declination. But bodies within the Solar System change their celestial positions.
The most important one to consider is the Sun. The Sun's declination can be found by measuring its altitude when it's on the meridian (at midday). The Sun's Right Ascension can be found by measuring the Local Sidereal Time of meridian transit. We find that the Sun's RA increases by approximately 4 minutes a day, and its declination varies between +23°26' and -23°26'. This path apparently followed by Sun is called the ecliptic.

The reason the Sun behaves this way is that the Earth's axis is tilted to its orbital plane.
The angle of tilt is
+23°26', which is called the obliquity of the ecliptic (symbol ε).
Any two great circles intersect at two nodes. The node where the Sun crosses the equator from south to north
(the ascending node) is called the vernal (or spring)
equinox. The Sun passes through this point around March 21st
each year.
This is the point from which R.A. is measured, so here
RA = 0h.
At RA = 12h, the descending node is called the
autumnal equinox; the Sun
passes through this point around September 23rd each year. At both these points, the Sun is on the equator, and spends 12 hours above horizon and 12 hours below.
("Equinox" means "equal night": night equal to day.)
The symbols used for the spring and autumn equinoxes,
 and
and
 are the astrological symbols for Aries and Libra.
are the astrological symbols for Aries and Libra.
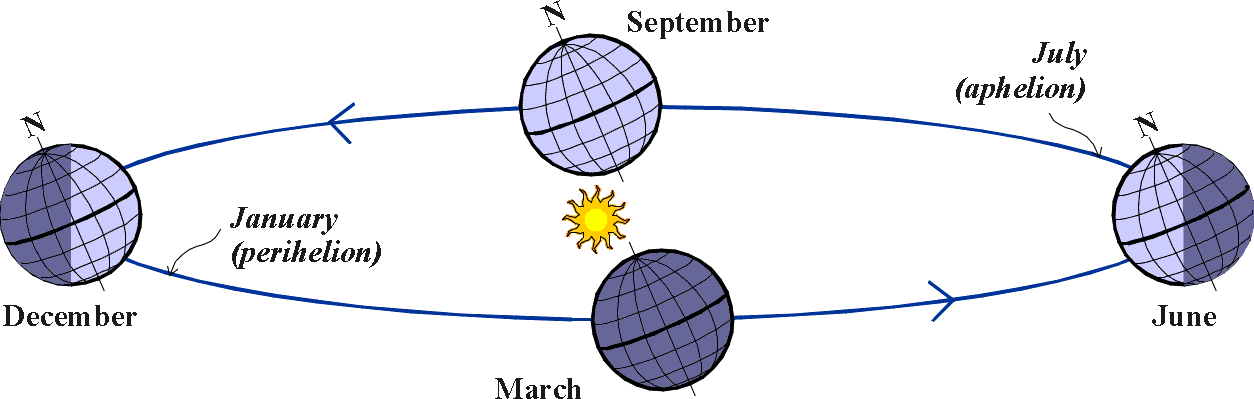
The most northerly point of the ecliptic is called (in the northern hemisphere) the Summer Solstice (RA = 6h): the Sun passes through this point around June 21st each year. The most southerly point is the Winter Solstice (RA = 18h); the Sun passes through this point around December 21st each year. At the northern Summer Solstice, the northern hemisphere of
Earth is tipped towards Sun,
giving longer hours of daylight and
warmer weather (despite the fact that Earth's slightly elliptical
orbit takes it furthest from the Sun in July!)
Thus the Sun's motion is simple when referred to the ecliptic; also the Moon and the planets move near to the ecliptic. So the ecliptic system is sometimes more useful than the equatorial system for solar-system objects.
تمرين:
The Moon’s orbit is tilted at 5°8' to the ecliptic. What is the lowest latitude from which the Moon may never set (the Moon’s “arctic circle”)?
Would the Moon always be circumpolar, at this latitude?
الحل:
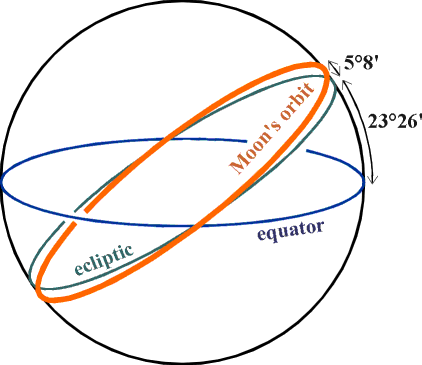
An object of declination δ
will be circumpolar
at latitude 90°-δ, i.e. at latitude
61°28'.
Would the Moon always be circumpolar, at this latitude?
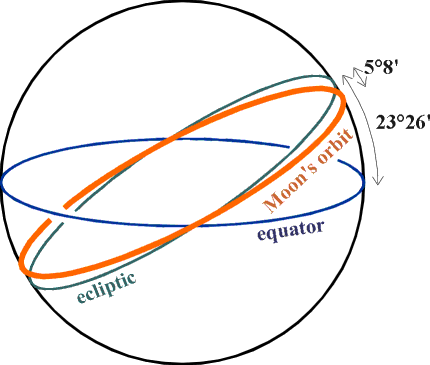
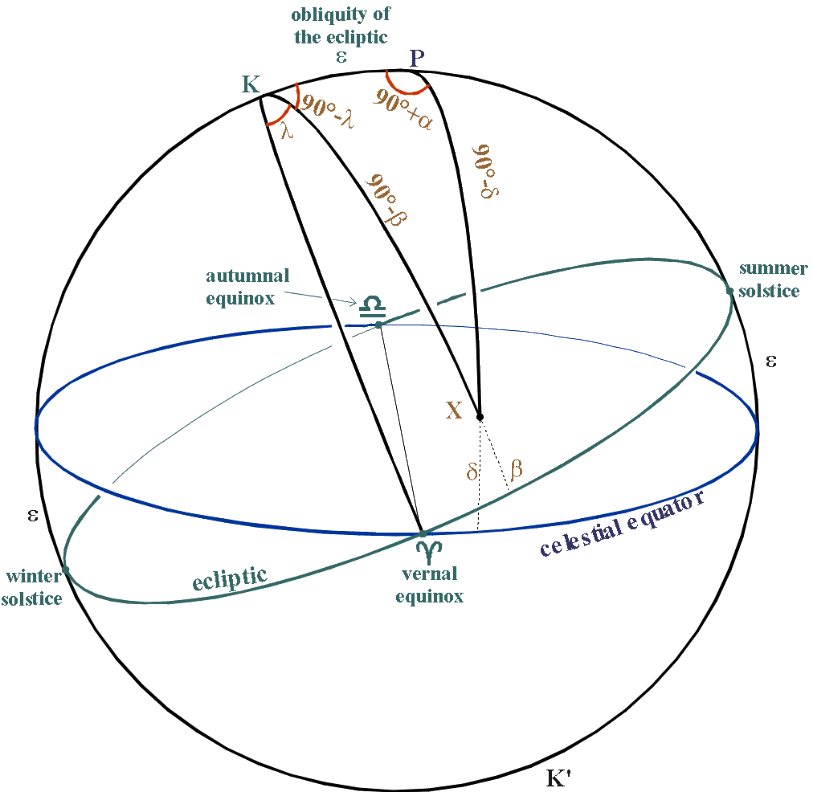
In the ecliptic system of coordinates, the fundamental great circle is the ecliptic. The zero-point is still the vernal equinox. Take K as the northern pole of the ecliptic, K' as the southern one.
To fix the ecliptic coordinates of an object X on the celestial sphere, draw the great circle from K to K' through X.
The ecliptic (or celestial) latitude of X (symbol β)
is the angular distance from the ecliptic to X,
measured from -90° at K' to +90° at K. Any point on the ecliptic has
ecliptic latitude 0°.
The ecliptic (or celestial) longitude of X (symbol λ)
is the angular distance along the ecliptic from the vernal
equinox to the great circle through X.
It is measured eastwards
(like R.A.), but in degrees, 0°-360°.
To convert between ecliptic and equatorial coordinates, use the spherical triangle KPX.
تمرين:
Show that, for any object on
the ecliptic, tan(δ) = sin(α)
tan(ε), where (α, δ)
are the object's Right Ascension and declination,
and ε
is the obliquity of the ecliptic.
الحل:
- احداثيات مجرية
ترجمة قتيبة أقرع
- تحويل بروجي استوائي